which just calls eval again!
When does it all end?

Eval calls apply,
which just calls eval again!
When does it all end?
In this project, you will develop an interpreter for a (slightly modified) subset of the Scheme language. As you proceed, think about the issues that arise in the design of a programming language; many quirks of languages are the byproduct of implementation decisions in interpreters and compilers.
You will also implement some small programs in Scheme, including the
count_change function that we studied in lecture. Scheme is a simple
but powerful functional language. You should find that much of what you have
learned about Python transfers cleanly to Scheme as well as to
other programming languages.
To learn more about Scheme, you can read Brian Harvey and
Matthew Wright's Simply Scheme textbook online for free.
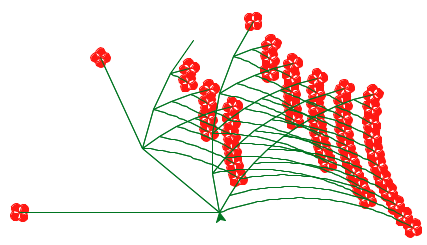
This project concludes with an open-ended graphics contest that challenges you to produce recursive images in only a few lines of Scheme. As an example of what you might create, the picture above abstractly depicts all the ways of making change for $0.50 using U.S. currency. All flowers appear at the end of a branch with length 50. Small angles in a branch indicate an additional coin, while large angles indicate a new currency denomination. In the contest, you too will have the chance to unleash your inner recursive artist.
This project includes several files, but all of your changes will be made to
the first three:
scheme.py,
tests.scm, and contest.scm. You can download all of the
project code as a zip archive.
scheme.py |
The Scheme evaluator |
tests.scm |
A set of small test cases and expected outputs for your interpreter |
contest.scm |
A place to write your contest entry |
scheme_tokens.py |
A Tokenizer for scheme |
scheme_primitives.py |
Defines primitive Scheme data structures and primitive functions via the Python Library |
scheme_prelude.scm |
A few more standard functions, defined in Scheme and read during initialization of the interpreter. |
scheme_test.py |
A testing framework for Scheme |
scheme_utils.py |
A few useful utilities. |
ucb.py |
Utility functions for 61A |
This is a three-part project. As in the previous project, you'll work in a team of two people, person A and person B. In each part, you will do some of the work separately, but most questions can be completed as a pair. Both partners should understand the solutions to all questions.
After completing the first (short) part, you will be able to read and parse Scheme expressions. In the second (long) part, you will develop the interpreter in stages:
let expression.
There are 30 possible points, along with 4 extra credit points. The extra credit problems are a bit involved; we recommend that you complete them all, but only after you have the regular stuff working. Finally, participants in the contest can earn up to 3 additional points, along with the glory of victory.
Before you begin working on the project, review what you have learned in
lecture about the Scheme
language. If you would like to experiment with a working Scheme
interpreter, look at Stk, which is
installed on instructional machines as stk.
We've implemented some standard Scheme procedures in Scheme, and you
can look at these for examples. They are in the file scheme_prelude.scm.
(The term standard prelude refers to any such collection of
definitions that is (at least in effect) executed to establish
standard definitions before any program is run.)
Read-Eval-Print. Run interactively, our interpreter reads
Scheme expressions from the terminal (the standard input, to be precise),
evaluates them, and
prints the results.
Our interpreter
uses scm> as the prompt.
The starter code for your Scheme interpreter in scheme.py can
successfully evaluate this simple expression, since it consists of a single
literal numeral. The rest of the examples in this section will not
work until you complete various portions of the project.
Certain expressions are given no specified value in the Scheme standard.
The STk interpreter (annoyingly, in my opinion) prints okay for some
of these and prints various random things for others (for example, it prints
the symbol just defined as the value of the define expression.)
Our interpreter, by contrast, returns a special value
(called UNSPEC in the Python code) that the read-eval-print loop
does not print (likewise, our Python interpreter does not
print None; however UNSPEC is not intended to be used
in programs, unlike None.)
Non-standard Symbols. Our Scheme subset does not have strings.
Instead, we use Scheme symbols for this purpose. Officially, symbols in
Scheme need only support a limited set of characters. For example, whitespace,
parentheses, and apostrophes are not part of this set, for the obvious reason
that they have other lexical significance as delimiters in Scheme. However, Scheme
dialects are allowed to introduce various extensions that allow extended
symbols containing arbitrary characters. In our dialect, you can create
non-standard symbols using "|" (vertical bar) as the quotation character.
Within such symbols, you can use the standard Python backslash-escapes, with
the addition of \|, which is how one includes a vertical bar
in a non-standard symbol. When printed using the standard Scheme function
display, the symbols are printed without the quotes and with
the escape sequences translated. For example,
Non-standard Functions.
Load. Our load function differs from standard Scheme in that, since we
don't have strings, we use a symbol for the file name. For example
Exiting. The functions bye or exit
terminate the interpreter. They allow an extra numeric argument giving the
Unix exit code (0 for normal exit, non-zero otherwise).
Words and Sentences. Mostly for the heck of it, we've added a number of functions from the Simply Scheme extensions used in courses at Berkeley. Specifically:
(sentence A B ...) concatenates lists, but also allows
symbols and numbers as arguments, treating these as one-element lists.
(word A B ...) concatenates the string representations of
the symbols and numbers A, B, etc. into a new symbol or number.
(first A) the first item in (car of) A if it a list, or a symbol or
number consisting of the first character in A's representation, if A is
symbol or number.
(last A) the last item in A if it a list, or a symbol or
number consisting of the last character in A's representation, if A is
symbol or number.
(butfirst A) if A is a list, its cdr, and otherwise
if it is a symbol or number, the symbol or number consisting of all but the
first character in A's repreentation (abbreviation: bf)
(butlast A) if A is a list, the list consisting of all but
its last element, and otherwise
if it is a symbol or number, the symbol or number consisting of all but the
last character in A's repreentation (abbreviation: bl).
Turtle Graphics. Finally, to keep up the traditions of recent years, we've added some
simple routines for turtle graphics, described later,
that simply call functions in the
Python turtle package (whose
documentation we
suggest you see; for one thing, it will let you try out turtle-graphics programs
in Python).
This time, we're letting you come up with tests. As you complete
each problem, add tests to the file tests.scm of the
constructs you have implemented.
expressions that you can examine and test to become more familiar with the
language. Each line that prints output is followed by the expected result as a
comment.
You can run all commands in a file using your Scheme interpreter by passing
the file name as an argument to scheme.py.
scheme_test.py.
tests.scm contains
Scheme expressions interspersed with comments in the form
scheme_test script collects these expected outputs and compares
them with the actual output from the program, counting and reporting mismatches.
You can even test that your interpreter catches errors. The problem with
error tests is that there is no "right" output. Our script, therefore,
only requires that error messages start with "Error". Any such
line will match
tests.scm file.
Don't forget to use the trace decorator from the ucb
module to follow the path of execution in your interpreter.
As you develop your Scheme interpreter, you may find that Python raises
various uncaught exceptions when evaluating Scheme expressions. As a result,
your Scheme interpreter will crash. Some of these may be the results of bugs
in your program, and some may be useful indications of errors in user programs.
The former should be fixed (of course!) and the latter should be caught
and changed into SchemeError exceptions,
which are caught and printed as error messages by the Scheme read-eval-print
loop we've written for you. Python exceptions that "leak out" to the user
in raw form
are errors in your interpreter (tracebacks are for implementors, not civilians).
This project is about modifying a modestly complex piece of existing code.
In such a situation, it's good to take time at the outset to read what's
provided, try to understand what's there, and accumulate questions about parts
you don't understand before trying to mess around with it. Indeed,
a lot of what you take away from this project will simply be what you learn
by reading all the code you don't have to write.
In many
cases, you'll be able to experiment with parts of it in isolation, simply by
starting up an interactive Python session and using import to
get access to the parts you'd like to play with.
Take a look over all the files provided with this project (with
your partner, of course). Look particularly at
scheme_primitives.py, which defines the basic data
structures that Scheme programs manipulate (subclasses of
SchemeValue), and at the classes in
scheme.py that define the Scheme values devoted to
functions (subclasses LambdaFunction (for functions defined
with lambda and define) and
PrimitiveFunction (for functions implemented directly in
Python). The implementations of primitive functions in
scheme_primitives.py may be useful to you in
understanding how these data structures work.
In the file scheme.py, look at read_eval_print, which
is the top-level function that defines the interpreter's actions.
Look also at the class EnvironFrame, which represents environment frames
(just like those in the text and in lecture). Look at the run
function and what it calls to see how the interpreter gets initialized and
how the global environment comes to be.
You won't have to modify scheme_tokens.py, but since you will
be modifying the reader (and since we can ask you anything we want on tests),
it might be a good idea to understand the routines it provides and how they
are used. At any given time, the "current port" is a Buffer
(see scheme_utils.py), which is used to
provide a continuous stream of tokens from a token source. See if you can
figure out how to look at the token stream produced for a small Scheme file.
Finally, it would be a good idea to start trying to understand
evaluation, which is concentrated in the class Evaluation
in scheme.py.
The function scm_read in scheme.py is intended to
read Scheme expressions from the "current port" (input source) and return them
in their internal form (as various types of SchemeValue). At the
moment, it only handles numbers, symbols, boolean values, and the end of file.
Problem 1 (2 pt). Your first task, with your partner, is to complete
scm_read by filling in the portions
responsible for reading pairs, lists, and items quoted by the apostrophe
(the reader is supposed to treat 'S as a synonym for
(quote S)).
The syntax for pairs and lists is a left parenthesis, followed by a "tail", defined as
The nested function read_tail reads the tail, returning its value.
For example, the value returned for "(1 2 . 3)" consists of
the value of the tail "1 2 . 3)", which is
1 and the value of the tail "2 . 3)", which is
2 and the Scheme
value 3.
Pair(Number(1), Pair(Number(2), Number(3))).
As another example, the value returned for "(1 2)" is the value of
the tail "1 2)", which is
1 and the value of the tail "2)", which is
2 and the value
of the tail ")", which is the empty list.
Pair(Number(1), Pair(Number(2), NULL)).
You'll be able to test the resulting reader by easily enough, since the initial project simply prints the Scheme expressions that it reads without evaluating them, so a Unix command like
tests.scm (or any other file full of Scheme
expressions), convert them to internal Scheme values,
and print out these values.
The heart of the evaluator is the class Evaluation, which
corresponds roughly to those round-cornered boxes containing expressions and
values with links to environment frames:
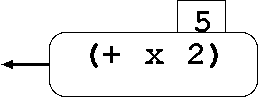
That is, an Evaluation contains an expression being evaluated and
the environment in which to evaluate it, or else (if .evaluated()
is true) a value that requires no further evaluation. Each call to
the .step() method on an Evaluation makes some
progress towards a final value: either it finishes the evaluation (so that
.evaluated() becomes true), or it performs some of the evaluation,
and replaces its expression and environment with new ones that, if evaluated,
will complete the evaluation.
We do it this way to make tail-recursive programs into iterative ones
(Python implementations will eventually run out of space if they pursue
a tail-recursive program too far, whereas in Scheme programs, tail recursion
is supposed to be the same as iteration). For example, if the expression
to be evaluated is a call on a primitive function, then one evaluation step
will evaluate the arguments and call the primitive function, completing the
evaluation. However, if the expression is a call on a user-defined function,
then an evaluation step will evaluate the arguments of the call, then
replace the Evaluation's expression with the body of the
user-defined function, and its environment with a new local environment
defining the parameters (just as we showed in lecture long ago for
Python). Subsequent evaluation steps will evaluate the body. Take a look
at the code for the begin special form (do_begin_form)
for a simple example of evaluating a list of expressions, returning the
value of the last one.
Problem 2.
First, follow the directions in scm_eval to make it
actually evaluate expressions as intended.
Problem A2 (2 pt). Now we are going to get simple symbol evaluation and
definition to work. The first part is to handle the missing symbol case in
Evaluation.step. Fill this in to properly evaluate
expr when it consists of a single Scheme symbol.
There are
a few values you'll be able to look at: the values of primitive functions,
such as +.
Problem B2 (2 pt).
There are two missing parts in the method do_define_form, which
handles the (define ...) construct. Here, we'll do just
the first part: handling cases like
Now that you can created symbols and give them simple values, it should
be easy to come up with tests for A2 and B2 to add to tests.scm.
Problem 3 (2 pt).
The function do_call_form is
supposed to evaluate a function call. It does so by evaluating the
operands of the call and then using the apply_step
method, which is supposed to be defined for the first, "operator", operand.
At the moment, however, it is incomplete. Instead, the provided implementation
just evaluates the operator, and then simply calls the
apply_step method on it with no arguments.
Also, neither of the apply_step bodies—that of
PrimitiveFunction and that of LambdaFunction—are
complete. Instead, they simply set the Evaluation they are
passed so that it immediately evaluates to #f (false).
Implement do_call_form and
PrimitiveFunction.apply_step
correctly. After you're finished, your evaluator should be able
to evaluate calls on primitive functions.
For example, you should see the following results:
As always, your implementation should check for errors in the input line! A call such as
apply_step procedure to raise a SchemeError, which the read_eval_print function will duly report.
It turns out to be easy to arrange for this. The
quotient is implemented as a call to the Python function
scm_quotient. You might see what Python does when you call a
function with the wrong number of arguments and figure out how you can use that
to solve the problem of detecting and properly reporting errors.
Be sure you've added tests to tests.scm for what you've
implemented.
Problem 4. Now we turn to user-defined functions, represented by
values of type LambdaFunction. When you've finished
parts A4 and B4, you should be able to enable the commented-out part of
create_global_environment, so that initialization of the
interpreter will read in the Scheme prelude, a set of definitions of
standard functions written in Scheme instead of Python.
Problem A4 (2 pt).
Before we can call LambdaFunctions, we must be
able to create them. At the moment, the do_lambda_form
method, which creates LambdaFunction values, is incomplete.
Finish it. You can check your work by typing in lambda expressions to
the interpreter. You should see something like this:
begin is inserted, see the
__init__ function for the LambdaFunction class.
Problem B4 (2 pt). The part of do_define_form that you
didn't do in B2 handles the shorthand form for defining functions, allowing
you to write
Fill in this missing portion of do_define_form.
Problem A5 (3 pt).
The make_call_frame method
of EnvironFrame is incomplete. Finish it.
Don't forget the cases where the formal parameter list contains a trailing "varargs" entry, as in
(1 2 3) has the internal structure
(a . b) has the structure
a to the number 1
and symbol b
to Pair(number, Pair(number, NULL))
Likewise, the ordinary formals list (a b c) has the structure
Problem B5 (3 pt).
Likewise, check_formals, the method that checks the
formals-list argument to make_call_frame, does nothing at the
moment. Fix it so that make_call_frame can assume that
its "formals" argument is correctly formed.
Problem 6 (3 pt).
At this point, you should be able to get user-defined functions working
by filling in LambdaFunction.apply_step.
Be sure to add tests for Problems 4–6 to tests.scm
Problem 7 (2 pt). Fill in the implementation of
do_set_bang_form, which handles the set!
special form. Be sure to include a check that it has the proper form and that
the symbol being assigned to is defined. And, as usual, be sure to have
tests in tests.scm
Problem 8.
The basic Scheme conditional constructs are
if, and, or, and cond.
In order to handle tail recursion properly, all these methods must be careful
how they perform their evaluations. For example, consider the following
tail-recursive function
do_cond_form method were to evaluate the recursive call,
then the Python interpreter would have an ever-increasing call depth as it
"cdred" down the list, eventually blowing up if the list were long enough.
So instead, do_cond_form (and the other conditional forms) must
use the option of modifying the expression to be evaluated and then returning
without actually doing the evaluation.
Problem A8 (3 pt).
For the first half of the problem, fill in the implementations of
do_if_form
and do_and_form and test them.
Problem B8 (3 pt). For the second half, fill in the
implementations of
do_cond_form and do_or_form and test them.
Problem 9 (3 pt).
The let special form introduces local variables, giving them
their initial values. For example,
let statement above is equivalent to the call
x and y are separate from the outer
ones, and the initialization expressions in the let construct do
not reference the local variables x and y.
Implement the do_let_form method to have this effect and
(need we say it at this point?) test it.
Extra Credit 1. (2 pt).
The let* construct is like let, except that
each initialization expression "sees" the definitions that have gone
before. Essentially,
(11 15), rather than
(11 8), as it would for let. Implement this
special form (and, yes, test it).
Extra Credit 2 (2 pt).
The case construct is a fancy conditional similar to the
Java and C/C++ switch statement. Here are some examples from
the Scheme reference manual:
cond the remaining items in the matching operand are evaluated,
and the value of the last is the value of the case. Implement
and test this special form.
You should have been adding tests to tests.scm as you
did each problem. In any case, make sure you have a reasonably complete
set, since the readers will be looking at it. Your program should pass all
your tests when you (or the autograder) run
# python3 scheme_tests.py tests.scm
Your Scheme interpreter implementation is now complete.
Not only is your Scheme interpreter itself a tree-recursive program, but it is
flexible enough to evaluate other recursive programs. Implement the
following procedures in Scheme at the bottom of tests.scm, along with some calls and
expected results.
Problem 10. The first problems (one for you and one for your
partner) ask you to implement some familiar operations
destructively.
That means that the cdrs of the original list may be
changed and no new pairs should be created with cons or
list. There's a definition of non-destructive reverse
in scheme_prelude.scm and there are implementations of
filter on Python rlists in
Lecture 9. To see the desired difference between destructive and non-destructive
operations, consider:
Problem A10 (3 pt). Implement the filter! procedure, which
takes two arguments, a procedure name and a list and
destructively returns a list
that contains all elements of the input list for which applying the named
procedure outputs a true value (i.e., something other than #f).
Make your program tail recursive. It is easy to do this if you use
your partner's reverse! function. Try instead to implement it
directly.
Problem B10 (3 pt). Implement the reverse! procedure, whic
takes a list and returns the reverse of that list destructively.
Problem A11 (2 pt). Implement the count-change procedure,
which counts all of the ways to make change for a total amount,
using coins with various denominations (denoms), but never uses
more than max-coins in total. Write your implementation in
tests.scm. The procedure definition line is provided, along with
U.S. denominations.
Problem B11 (2 pt) Implement the count-partitions
procedure, which counts all the ways to partition a positive integer
total using only pieces less than or equal to another positive
integer max-value. The number 5 has 5 partitions using
pieces up to a max-value of 3:
Problem 12 (3 pt). Implement the list-partitions
procedure, which lists all of the ways to partition a positive integer
total into at most max-pieces pieces that are all
less than or equal to a positive integer max-value. Hint:
Define a helper function to construct partitions.
Congratulations! You have finished the final project for 61A! Assuming your tests are good and you've passed them all, consider yourself a proper computer scientist!
Get some sleep.We've added a number of primitive drawing procedures that are collectively
called "turtle graphics". The turtle represents the state of the drawing
module, which has a position, an orientation, a pen state (up or down), and a
pen color. The tcsm_x functions in
scheme_primitives.py are the implementations of these
procedures, and show their parameters with a brief description of each.
The Python documentation of
the turtle module contains more detail.
Contest (3 pt). Create a visualization of an iterative or recursive process of your choosing, using turtle graphics. Your implementation must be written entirely in Scheme, using the interpreter you have built (no fair extending the interpreter to do your work in Python, but you can expose other turtle graphics functions from Python if you wish).
Prizes will be awarded for the winning entry in each of the following categories.
Entries (code and results) will be posted online, and winners will be selected by popular vote. The voting instructions will read:
Please vote for your favorite entry in this semester's 61A Recursion Exposition contest. The winner should exemplify the principles of elegance, beauty, and abstraction that are prized in the Berkeley computer science curriculum. As an academic community, we should strive to recognize and reward merit and achievement (translation: please don't just vote for your friends).
To improve your chance of success, you are welcome to include a title and
descriptive haiku in the
comments of your entry, which will be included in the voting.
Place your completed entry into the contest.scm file.