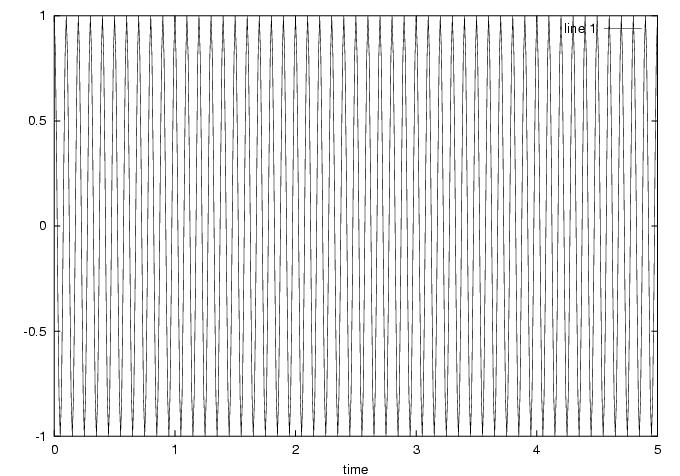
10 Hz cosine:

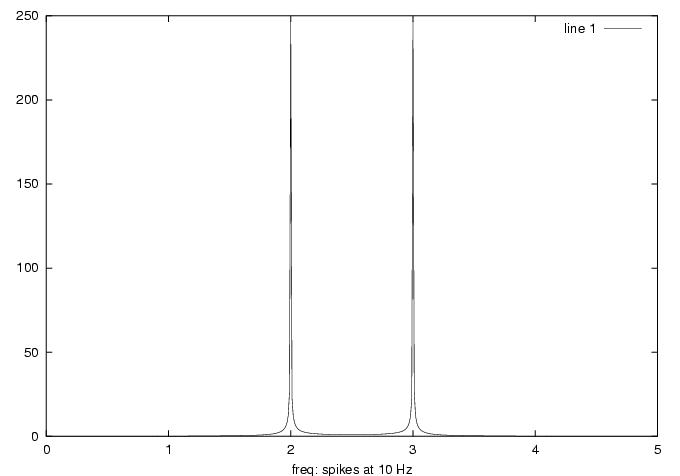
DFT of 10 Hz cosine:
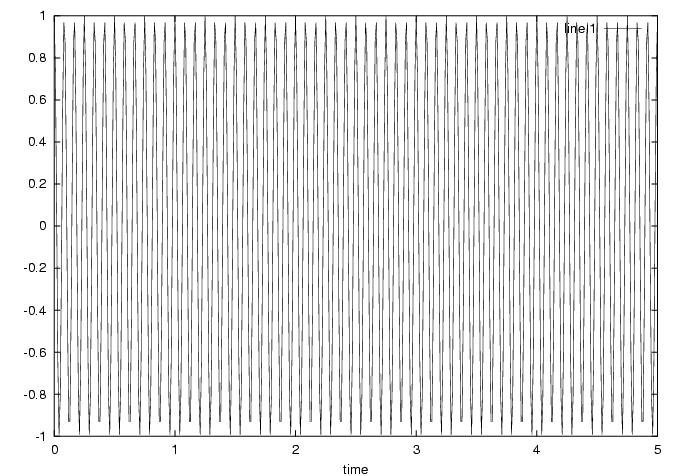
12 Hz cosine:
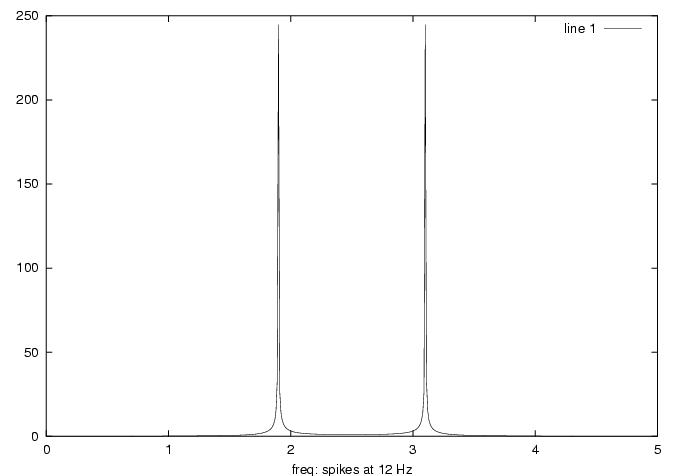
DFT of 12 Hz cosine:
Multiplication of 10 Hz and 12 Hz cosines:
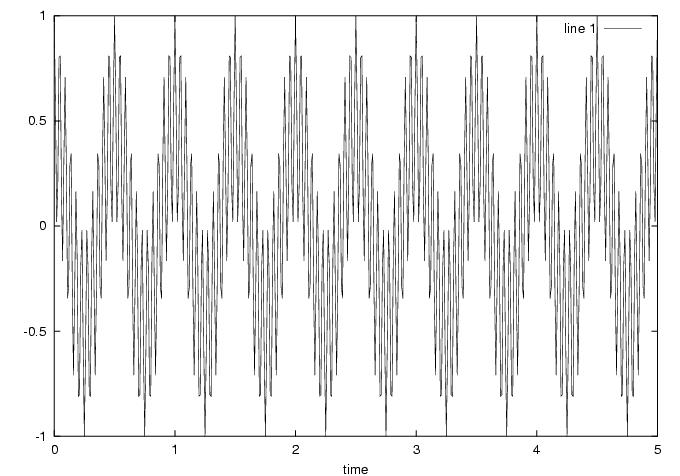
Note that there is an overall frequency of 12-10 = 2 Hz with an internal oscillation at 10+12 = 22 Hz.
DFT of multiplication of 10 Hz and 12 Hz cosines:

Here we have spikes at (12-10) = 2 Hz and (12+10) = 22 Hz. We can verify this by graphically convolving the 10 Hz spike with the 12 Hz spike. Since the multiplication we saw in the time domain affected the frequency, we see both the low (2 Hz) and high (22 Hz) frequencies in the DFT.
Sum of 10 Hz and 12 Hz cosines:
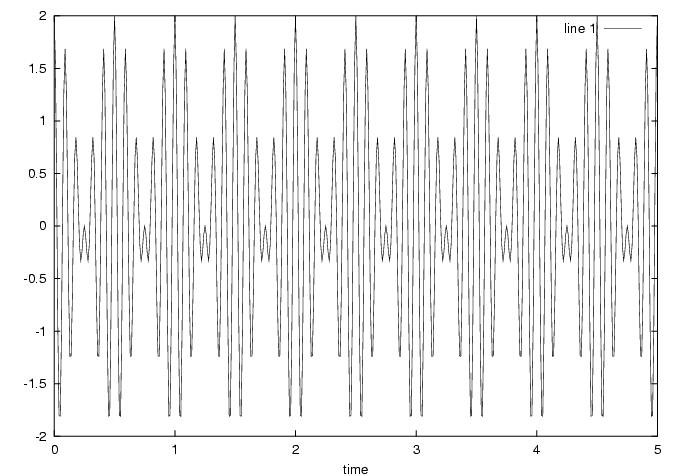
Note the amplitude modulation at 12-10 Hz. We see this in the form of an envelope in which the signal oscillates.
DFT of sum of 10 Hz and 12 Hz cosines:

Note the presence of both the 10 Hz and the 12 Hz spikes. This is because the DFT is a linear operator. The amplitude modulation at 2 Hz (= 12-10 Hz) that we note (or hear, in the case of musical sound waves) is due to constructive and destructive interference as the slightly different frequency waves have the effect of going in and out of phase with respect to one another. Since this affects the amplitude and not the frequency, we do not see a spike at 2 Hz in the freqency plot. Note also that the placement of the spikes (though not necessarily the magnitude) are the same as if we had multiplied two cosines with frequency (12-10)/2 = 1 Hz and (12+10)/2 = 11 Hz. (Check this! 11+1 = 12 Hz and 11-1 = 10 Hz)