Copy the directory ~cs61c/labs/07 to an appropriate place under your home directory.
If you recall, matrices are 2-dimensional data structures wherein each data element is accessed via two indices. To multiply two matrices, we can simply use 3 nested loops, assuming that matrices A, B, and C are all n-by-n and stored in one-dimensional column-major arrays:
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
for (int k = 0; k < n; k++)
C[i+j*n] += A[i+k*n] * B[k+j*n];
Matric multiplication operations are at the heart of many linear algebra algorithms, and efficient matrix multiplication is critical for many applications within the applied sciences.
In the above code, note that the loops are ordered i, j, k. Thus, considering the innermost "k" loop, we move through B with stride 1, A with stride n and C with stride 0. To compute the matrix multiplication correctly, the loop order doesn't matter. However, how we choose to stride though the matrices can have a large impact on performance as it can break the assumption of spacial locality that is critical for good cache performance.
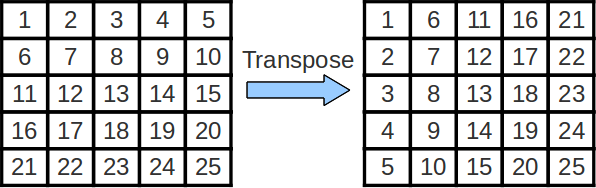
Sometimes, we wish to swap the rows and columns of a matrix. This operation is called a "transposition" and an efficient implementation can be quite helpful while performing more-complicated linear algebra operations. The transpose of matrix A is often denoted as AT.

In the above code for matrix multiplication, note that we are striding across the entire matrices to compute a single value of C. As such, we are constantly accessing new values from memory and obtain very little reuse of cached data! We can improve the amount of data reuse in cache by implementing a technique called cache blocking. More formally, cache blocking is a technique that attempts to reduce the cache miss rate by improving the temporal and/or spacial locality of memory accesses. In the case of matrix transposition we consider completing the transposition one block at a time.
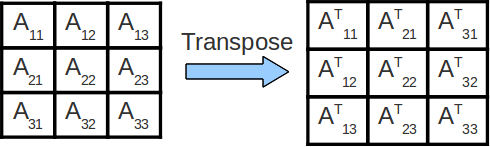
In the above image, each block Aij of matrix A is transposed into its final location in the output matrix. With this scheme, we significantly reduce the magnitude of the working set in cache at any one point in time. This (if implemented correctly) will result in a substantial improvement in performance. For this lab, you will implement a cache blocking scheme for matrix transposition and analyze its performance. As a side note, you will be required to implement several levels of cache blocking for matrix multiplication for Project 2.
Make sure you run the following on a machine in SDH 200! Take a glance at matrixMultiply.c. You'll notice that the file contains multiple implementations of matrix multiply with 3 nested loops. Compile and run this code with the following command: make ex1
Note that it is important here that we use the '-O3' flag to turn on compiler optimizations. The makefile will run matrixMultiply twice. Copy the results somewhere so that you do not have to run this program again and use them to help you answer the following questions:
Checkoff: Be prepared to explain your responses to the above questions to your TA.
Compile and run the naive matrix transposition implemented in transpose.c (make sure to use the '-O3' flag).
Checkoff: Show and explain your code to your TA. Answer the questions in part c above and then run your code with a block size of 30-by-30 to verify your algorithm works.
Please take the time to fill out the mid-semester survey. This IS a part of your checkoff for this lab. You can verify your submission using the submission verifier.
Checkoff: Show your submission verification to your TA.