Updates
- Extra credit removed. Moved to Project 5. More details eventually.
- Submission process updated
- 10/14 : Part 1 posted.
Background
A researcher in the UCB Parlab has been working on a video processing application that separates foreground and background information from video data. Unfortunately, he has little background in high-performance computing and needs your domain expertise to optimize the computational bottleneck of his code: a matrix multiply. Recall that matrix multiply is of this form:

Unfortunately for the researcher, his matrix multiply has certain characteristics that make it unsuitable for a canned library application. In particular, this matrix is single precision of dimension 1000 <= M <= 10000 rows and less than or equal to N=100 columns. Each of the columns represents a single video frame in grayscale, and the algorithm attempts to detect the background as pixels that do not change greatly from frame to frame.
The matrix multiply is of the form A * A’ where A’ is the transpose of A. This means that the resulting matrix is symmetric. However, you are required to compute all of the entries separately so that the Gflop/s benchmark accurately reflects the number of computations being performed. Faster results could definitely be achieved if this requirement were lifted.
The matrices are stored in column major format. The following diagram labels the matrices with their number of rows and columns, and represents a good way to visualize the problem:
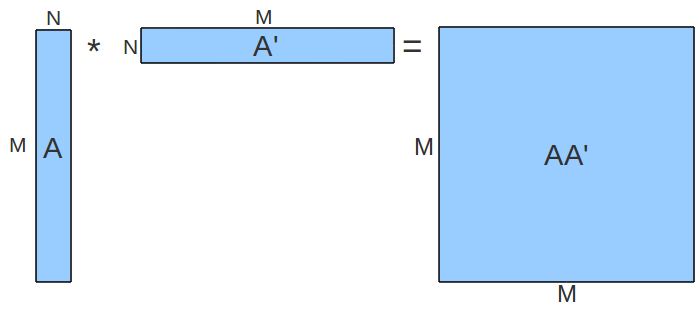
Your objective is to parallelize and optimize the matrix multiply operation described above!!! Awesome, right?
Architecture
What follows is information concerning the computers you will be working on. Some of it will be useful for specific parts of the project, but other elements are there to give you a real world example of the concepts you have been learning, so don't feel forced to use all of the information provided.
You will be developing on Mac Pros model 4,1. They are packing not one, but two Intel Xeon 5500 microprocessors (codename Gainstown). Each has 4 cores, for a total of 8 processors, and each core runs at a clock rate of 2.26 GHz.
Each core comes with 16 general purpose integer registers (though a few are reserved such as the stack pointer). They also have 16 XMM registers a piece for use with the SIMD intrinsics.
All caches deal with block sizes of 64 bytes. Each core has an L1 instruction and L1 data cache, both of 32 Kibibytes. A core also has a unified L2 cache (same cache for instructions and data) of 256 Kibibytes. The 4 cores on a microprocessor share an L3 cache of 8 Mibibytes. The associativities for the L1 instruction, L1 data, unified L2, and shared L3 caches are 4-way, 8-way, 8-way, and 16-way set associative, respectively.
Getting Started
For this project, you will be required to work in groups of two. You are not allowed to show your code to other students, teaching assistants, professors, loved ones, pets, or any other individuals. You are to write and debug your own code in groups of 2. Looking at solutions from previous semesters is also strictly prohibited.
To begin, pull the contents of the repo ~cs61c/proj/fa12/03
$ cd ~/work
$ git pull ~cs61c/proj/fa12/03 master
- Makefile: allows you to generate the required files using make
- benchmark.c: runs a basic performance and correctness test using a random matrix
- sgemm-naive.c: a sample program that multiplies a matrix by its transpose in an inefficient manner
You can compile the sample code by running make bench-naive in the project directory. You do not need to modify or submit any of the provided files. Instead, you will be submitting two new files called sgemm-small.c (for part 1) and sgemm-openmp.c (for part 2).
You are not permitted to use the following optimizations for either part of the project:
- Aligned Loads / Stores (you are allowed to use mm_loadu, but not mm_load)
- Optimizations specific to the fact that the product is of the form AA' (because our benchmark program is set to judge Gflop/s peformance under that assumption)
Please post all questions about this assignment to Piazza, or ask about them during office hours. Extra office hours will be held for the project, times for Part 2 are to be determined.
Part 1: Due Sunday, Oct 21, 2012 at 11:59PM (55pt)
Optimize a single precision AA' matrix multiply for a matrix of size 60x60. You are to compute the matrix C = AA'. Place your solution in a file called sgemm-small.c. You can create a template file by typing cp sgemm-naive.c sgemm-small.c. You will also need to add an appropriate #include directive before you can use SSE intrinsics. To compile your improved program, type make bench-small. You can develop on any machine that you choose, but your solution will be compiled using the given Makefile and will be graded on the Hive machines.
When you are done, for the part 1, create a file MYPARTNER.txt with your partner's login along with your submission and push your submission in the directory proj3 with the tag proj3-1.
Tune your solution for matrices of size 60x60. To receive full credit, your program needs to achieve a performance level of 10.5Gflop/s for matrices of this size. This requirement is worth 35pt. See the table below for details.
Your code must be able to handle small matrices of size other than 60x60 in a reasonably efficient manner. Your code will be tested on matrices with m=[32,100] and n=[32,300], and you will lose points if it fails to achieve an average of 5Gflop/s on such inputs. An effective way to avoid dealing with fringe cases is by padding the matrices with zeros so that they are of a more optimal size. This requirement is worth 20pt.
For this part, you are not allowed to use any other optimizations. In particular, you are not permitted to use OpenMP directives. Cache blocking will not help you at this stage, because 60x60 matrices fit entirely in the cache anyway (along with all other sizes we are testing in Part 1). Remember that aligned loads and AA' optimizations are prohibited for both parts.
We recommend that you implement your optimizations in the following order:
- Use SSE Instructions (see lab 8)
- Optimize loop ordering (see lab 7)
- Implement Register Blocking (load data into a register once and then use it several times)
- Implement Loop Unrolling (see lab 8)
- Compiler Tricks (minor modifications to your source code can cause the compiler to produce a faster program)
60x60 Matrix Grading
| Gflop/s | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 10.5 |
| Point Value | 1 | 4 | 7 | 10 | 15 | 20 | 25 | 30 | 32 | 34 | 35 |
Intermediate Gflop/s point values are linearly interpolated based on the point values of the two determined neighbors and then rounded to nearest integer. Rounding modes are to be determined. Note that heavy emphasis is placed on the middle Gflop/s, with the last couple being worth very few points. So don't sweat it if you are having trouble squeezing those last few floating point operations out of the machine!
Part 2: Due Sunday, Oct 28, 2012 at 11:59PM (55pt)
The Objective
Now that you have proved your valor on the eternal battlefield that is optimization it is time to test your mettle on a new beast of a problem. The stakes have increased but so has your arsenal. We will be dealing with much larger tall and skinny matrices from here on out, and in order to work with them efficiently you will need to use cache blocking. You will also need to parallelize your computation across multiple cores in order to meet the required goals.
Submission and Grading
Place your solution in a file called sgemm-openmp.c. Test it
using make bench-openmp.
Submit by pushing your submission in the directory proj3 with the tag proj3-2
For Part 2, we will grade your average performance over a range of tall and skinny matrices with m=[1000,10000] and n=[32,100]. We will try strange matrix sizes, such of powers-of-2 and primes...so be prepared. Any valid solution that achieves an average performance of 50Gflop/s without using prohibited optimizations (aligned loads and stores, the fact that we are doing AA') will receive full credit (55pt).
Testing
We will be disabling remote logins on a few of the machines early in this coming week to allow for reliable testing of your matrix multiply code.
Matrix Range Grading
| Average Gflop/s | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| Point Value | 0 | 5 | 10 | 15 | 25 | 35 | 45 | 50 | 55 |
Extra Credit
Extra Credit has been removed from this project. It will be moved to Project 5. More details eventually.
Optimization Details
What follows are some useful details for Part 1 and Part 2 of this project.
SSE Instructions
Your code will need to use SSE instructions to get good performance on the processors you are using. Your code should definitely use the _mm_add_ps, _mm_mul_ps, _mm_loadu_ps intrinsics as well as some subset of:
_mm_load1_ps, _mm_load_ss, _mm_storeu_ps, _mm_store_ss _mm_shuffle_ps, _mm_hadd_ps
Depending on how you choose to arrange data in registers and structure your computation, you may not need to use all of these intrinsics (such as _mm_hadd_ps or _mm_shuffle_ps). There are multiple ways to implement matrix multiply using SSE instructions that perform acceptably well. You probably don't want to use some of the newer SSE instructions, such as those that calculate dot products (though you are welcome to try!). You will need to figure out how to handle matrices for which N isn't divisible by 4 (the SSE register width in 32-bit floats), either by using fringes cases (which will probably need optimizing) or by padding the matrices.
To use the SSE instruction sets supported by the architecture we are on ( MMX, SSE, SSE2, SSE3, SSE4.1, SSE4.2 ) you need to include the header <nmmintrin.h> in your program.
Register Blocking
Your code should re-use values once they have been loaded into registers (both MMX and regular) as much as possible. By reusing values loaded from the A or B matrices in multiple calculations, you can reduce the total number of times each value is loaded from memory in the course of computing all the entries in C. To ensure that a value gets loaded into a register and reused instead of being loaded from memory repeatedly, you should assign it to a local variable and refer to it using that variable.
Loop Unrolling
Unroll the inner loop of your code to improve your utilization of the pipelined SSE multiplier and adder units, and also reduce the overhead of address calculation and loop condition checking. You can reduce the amount of address calculation necessary in the inner loop of your code by accessing memory using constant offsets, whenever possible.
Padding Matrices
As mentioned previously it is generally a good idea to pad your matrices to avoid having to deal with the fringe cases. This implies copying the entire matrix into a re-formatted buffer with no fringes (e.g. copy 3x4 matrice into 4x4 buffer). You should allocate this buffer on the heap. Be sure to fill the padded elements with zeros.
Cache Blocking
The first step is to implement cache blocking, i.e. loading chunks of the matrices and doing all the necessary work on them before moving on to the next chunks. The cache sizes listed in the Architecture section should come in handy here.
OpenMP
Once you have code that performs well for large matrices, it will be time to wield the formidable power offered to you by the machine's 8 cores. Use at least one OpenMP pragma statement to parallelize your computations.
Miscellaneous Tips
You may also wish to try copying small blocks of your matrix into contiguous chunks of memory or taking the transpose of the matrix in a precompute step in order to improve spatial locality.
References
- Goto, K., and van de Geijn, R. A. 2008.Anatomy of High-Performance Matrix Multiplication,ACM Transactions on Mathematical Software 34, 3, Article 12.
- Chellappa, S., Franchetti, F., and Püschel, M. 2008.How To Write Fast Numerical Code: A Small Introduction,Lecture Notes in Computer Science 5235, 196–259.
- Bilmes, et al.The PHiPAC (Portable High Performance ANSI C) Page for BLAS3 Compatible Fast Matrix Matrix Multiply.
- Lam, M. S., Rothberg, E. E, and Wolf, M. E. 1991.The Cache Performance and Optimization of Blocked Algorithms,ASPLOS'91, 63–74.
- Intel Instrinsics Guide (see Lab 7)
- Intel® 64 and IA-32 Architectures Optimization Reference Manual
- OpenMP reference sheet
- OpenMP Reference Page from LLNL