A. Intro

Download the code for Lab 22 and create a new Eclipse project out of it.

B. Building Intuition about Sorting Algorithms

Discussion: Sorting by Hand

Explain how you would sort a hand of 13 playing cards as your are dealt the cards one-by-one. Your hand should end up sorted by suit, and then by rank within a suit.

Then explain how you would sort a pile of 300 CS 61BL exams by two-letter login. If it's different than your card-sorting algorithm of the previous step, explain why.

Overview of Sorting Algorithms

Today we'll explore several algorithms for sorting a collection of data. The methods we'll be working with will sort an array or linked list of integers, but the same ideas can be easily adapted to work with any kind of collection of Comparable objects.

There are several kinds of sorting algorithms, each of which is appropriate for different situations. At the highest level, we will distinguish between two types of sorting algorithms:

• Comparison sorts, which rely on making pairwise comparisons between elements in order to sort them.
• Distribution sorts, which group elements based on their "digits", and then sort and combine the groups. Distribution sorts do not need to compare individual elements to each other.

In this lab, we'll be covering a few different varieties of comparison sorts. Distribution sorts will wait until next lab.

Activities for today will include coding and analysis.

C. Insertion Sorts

Insertion Sort

The first sort type of comparison sort we'll learn is called an insertion sort. The basic idea for insertion sort can be summed up as follows:

1. Start a loop over all items in your collection.
2. For each item you find, insert it into its correct place among all the items you've looked at so far.

You might have intuited insertion sort when we asked you how to sort cards. This is like when you sort cards by continually putting the next card in the right spot in a group of sorted cards that you're holding.

(You were briefly introduced to this algorithm back when you were learning about arrays and loop invariants). Here is code that applies the insertion sort algorithm (to sort from small to large) to an array named arr.

public static void insertionSort (int[] arr) {
    for (int i = 1; i < arr.length; i++) {
        for (int j = i; j > 0 && arr[j] < arr[j - 1]; j--) {
            swap(arr, j, j - 1);
        }
    }
}

Self-test: When is Insertion Sort Awesome/Terrible?

For the below self-test, analyze the insertionSort code given above carefully. In particular, consider the comparison step in the for loop condition.

Assume we have an array with a million elements. What would the array have to look like before we ran insertion sort that would make insertion sort run the fastest (i.e. minimizing the number of comparisons made)?

What ordering would maximize the number of comparisons (and result in the slowest runtime)?

Exercise: Code Linked List Insertion Sort

We gave you the code for insertion sort on an array. To test if you understand the algorithm, try applying it to a linked list. The file IntList.java contains an implementation of a doubly-linked list, along with methods for sorting the list values. Supply the body of the insert method to complete the coding of the insertion sort algorithm.

Insertion Sort Variation: Tree Sort

For insertion sort, in pseudo code is

For each element in the collection to be sorted,
    insert it into its proper place in another collection.

The insertion sort algorithm we just considered did its insertion in an array, where elements had to be shifted over to make room for the new elements. Choice of a structure that allows faster insertion — namedly, a binary search tree — produces a faster algorithm. Recall that insertion into a binary search tree runs in time logarithmic with the number of items, in comparison with insertion into an array which is linear.

So, an alternative to insertion sort is to first build the tree through repeated insertions, and then at the end then traverse it in linear time to produce the sorted sequence. This variant of insertion sort is called tree sort.

D. Selection Sorts

Selection Sort

The selection sort algorithm, applied to a collection of N elements, involves the following kind of loop:

for (int i = 0; i < N; i++) {
    find and remove the smallest element remaining in the collection,
    and add it to the end of another sorted collection.
}

Given below is an implementations of the selection sort algorithm for arrays. You can also see a version for linked lists completed in IntList.java.

Array selection sort

for (int k = 0; k < values.length; k++) {
    // Elements 0 ... k-1 are in their proper positions
    // in sorted order.
    int minSoFar = values[k];
    int minIndex = k;
    // Find the smallest element among elements k ... N-1.
    for (int j = k+1; j < values.length; j++) {
        if (values[j] < minSoFar) {
            minSoFar = values[j];
            minIndex = j;
        }
    }
    // Put the element in its proper place.
    // Elements 0 ... k are now in their proper positions.
    swap (values, minIndex, k);
}

Self-test: Selection Sort Runtime

Analyze the code for selection sort carefully. Like insertion sort, is selection sort faster if the array starts off already sorted?

Calculate the asymptotic runtime of selection sort, in its different case(s). How does it compare with insertion sort?

N-1 + N-2 + ... + 1 = N*(N-1)/2

Selection Sort Variation: Heap Sort

Recall the basic structure for selection sort

for (int i = 0; i < N; i++) {
    find and remove the smallest element in the collection,
    and add it to the end of another sorted collection.
}

Adding something to the end of a sorted array or linked list can be done in constant time. What hurt our runtime was finding the smallest element in the collection, which always took linear time in an array.

Is there a data structure we can use that allows us to find and remove the smallest element quickly? A min heap fills the bill; removal of the largest element from a heap of N elements can be done in time proportional to log N! So, once the heap is created, sorting can be done in time proportional to N log N. (N removals from the heap are done, each taking time at worst proportional to log N.)

Recall that we can build a heap to start off with in linear time using the heapify algorithm (introduced in the heaps lab). This step is only done once, so it doesn't make our overall runtime worse than N log N. Pretty cool, huh? It turns out selection sort isn't so useless after all. Though, this type of sort is often give its own name, heap sort.

E. A Divide-and-Conquer Algorithm: Merge Sort

The sorting algorithms we just went through, insertion sort and selection sort, have at their basis the structure of iterating through each item in the collection one-by-one. There is another class of comparison algorithms, however, that does not take this approach.

"Divide and Conquer"

Another way to speed up sorting is by using a "divide and conquer" technique:

1. split the elements to be sorted into two collections.
2. sort each collection recursively.
3. combine the sorted collections.

Compared to selection sort, which involves comparing every element with every other, this dividing and conquering has the potential to reduce the number of comparisons significantly.

Two algorithms that apply this approach are merge sort and Quicksort.

Merge Sort

Merge sort works as follows.

1. Split the collection to be sorted in half somehow.
2. Sort each half. (This is recursive)
3. Merge the sorted half-lists.

The reason merge sort is fast is that merging two lists that are already sorted takes linear time proportional to the sum of the lengths of the two lists in the worst case. Splitting the collection in half requires a single pass through the elements. The processing pattern is depicted in the diagram below.

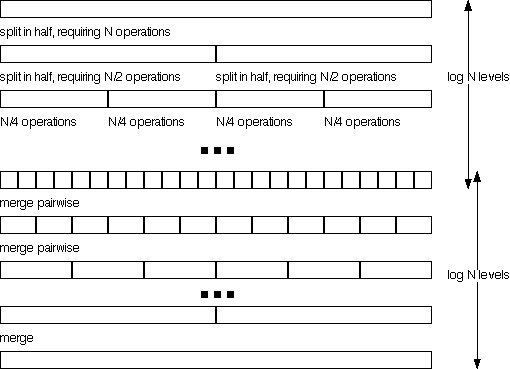
Each level in the diagram is a collection of processes that all together run in linear time. Since there are 2 log₂N levels, the total time is proportional to N log N.

Exercise: Code Linked List Merge Sort

To test your understanding of merge sort, fill out the mergeSort method in IntList.java. Be sure to take advantage of the provided merge method! We gave it to you so you don't have to write this again — do you remember writing it for an earlier lab?

F. Another Divide-and-Conquer Algorithm: Quicksort

Quicksort

Another example of dividing and conquering is the Quicksort algorithm:

1. Split the collection to be sorted into two collections by partitioning around a "divider" element (sometimes called the pivot). One collection consists of elements smaller than the divider, the other elements greater than or equal to the divider.
2. Quicksort the two subcollections.
3. Concatenate the sorted small values with the divider, and then with the sorted large values.

Here's an example of how this might work, sorting an array containing 3, 1, 4, 5, 9, 2, 8, 6.

1. Choose 3 as the divider. (We'll explore how to choose the divider shortly.)
2. Put 4, 5, 9, 8, and 6 into the "large" collection and 1 and 2 into the "small" collection.
3. Sort the large collection into 4, 5, 6, 8, 9; sort the small collection into 1, 2; combine the two collections with the divider to get 1, 2, 3, 4, 5, 6, 8, 9.

Concatenation in an array or linked list can be done in constant time. If partitioning can be done in time proportional to the number of elements N, and it splits the collection more or less in half, this produces an algorithm that runs in time proportional to N log N. (Reasoning is similar to what we used for merge sort.)

You can find a nice interactive demo of quicksort here

Exercise: Quicksort a Linked List

First, switch which partner is coding for this lab if you haven't already.

Some of the code is missing from the quicksort method in IntList.java. Supply it to complete the Quicksort implementation.

Be sure to use the supplied helper methods! They will make your job a lot easier.

Self-test: Worst Case Behaviour for a Quicksort

Unlike merge sort, Quicksort has a worst-case that makes it run in time worse than proportional to N log N. Suppose we always decided to make our pivot divider element the first element in the list. Then, which of the following initial conditions for the array would cause quicksort to exibit N² behavior?

Discussion: Picking the Divider

The median element would be the best divider for Quicksort. Describe an algorithm to find the median element. What is its runtime? It's okay if you think your solution isn't the most efficient.

Practical Methods for Selecting the Divider

How fast was the median-finding algorithm that you came up with? Finding the exact median of our elements may take so much time that it may not help the overall runtime of quicksort at all. It may be worth it to choose an approximate median, if we can do so really quickly. Options include picking a random element, or picking the median of the first, middle, and last elements. These will at least avoid the worst case discussed in the self-test.

Quicksort Performance in Practice

For reasons that can't be explained with our asymptotic runtimes, in practice Quicksort turns out to be the fastest of the general-purpose sorting algorithms we have covered so far (hence its name). For this reason, it's the algorithm used in Java's Arrays.sort method. With some tuning, the most likely worst-case scenarios are avoided, and the average case performance is excellent.

Here are some improvements to the basic Quicksort algorithm Java uses.

• When the number of items to sort gets small (the base case of the recursion), insertion sort is used instead
• For larger arrays, more effort is expended on finding a good divider element.
• Various machine-dependent methods are used to optimize the partitioning algorithm and the swap operation
• You can use dual pivots to generally speed up quicksort. Java actually uses it to implement the sort method for their Array data structure. You can learn more here

Java actually uses a hybrid merge/insertion sort called Timsort for its Collections.sort method, however, instead of a hybrid Quicksort/insertion sort. The reason for this — Quicksort's major weakness — will be revealed next lab.

Observe the general theme here: the simpler sorts (like insertion sort) tend to work better on small amounts of data, whereas the effectiveness of the more complicated sorts (merge sort and Quicksort) only kicks in on larger amounts of data.

G. Analyzing the Sorts

Identifying Mystery Sorts

This activity involves the use of a program called "Sort Detective" to identify "mystery" sort methods from their execution. (Credit for Sort Detective goes to David Levine, Computer Science Department, St. Bonaventure University, New York.) Note that this only runs on lab computers. To use this remotely, you will need to use X-forwarding, a feature that will allow windows created remotely to be forwarded and displayed to your local computer. To set this up;

• Mac/Unix: Simply use ssh -X instead of ssh. Mac users may first have to download X11.
• Windows: Set up X-forwarding following the steps here

The sort detecive program is included in the code for this lab. cd to the sort.detective directory and run Sort Detective:

(In lab22 directory)
cd sort.detective
java SortDetective

The five buttons on the left correspond to the insertion sort, selection sort, merge sort, Quicksort, and heap sort algorithms. (The tested implementations are given in the file sort.detective/allSorts.txt) Your task is to find out which button goes with which sort.

Create a list to be sorted by selecting relevant radio buttons and then clicking on "Create list". Then run one or more of the sorting methods on that list. Identify the sorting methods by observing their execution behavior on large and small lists, and already-ordered and randomly ordered lists.

Exercise: Sorting out the Sorts

In a file detective.txt, write down which button corresponds to which sorting algorithm. For each, explain how you determined it.

Animations

There are a lot of web sites that provide animations of sorting algorithms. Here are some good ones, including, but not limited to, ones we've already introduced:

• Animation of merge sort
• Good animations for seeing how sorts work with various problem sizes and initial data set states, such as random or nearly sorted
• Another site with a bunch of animations for sorting algorithms, among other things.
• A bit like the previously listed ones, but pretty
• Good interactive demo for quicksort

H. Conclusion

Submission

For lab22, turn in the completed IntList.java and detective.txt.

Reading

For next lab, reading DSA chapter 11.3 and 11.5 (Sorting and Selection).