A. Intro
Download the code for Lab 19 and create a new Eclipse project out of it.
B. Representing a tree with an array
Representing a Tree with an Array
You've seen two approaches to implementing a sequence data structure: either using an array, or using linked nodes. We extended our idea of linked nodes to implement a tree data structure. It turns out we can also use an array to represent a tree.
Here's how we implement a binary tree:
- The root of the tree will be in position 1 of the array (nothing is at position 0). We can define the position of every other node in the tree recursively:
- The left child of a node at position
nis at position2n. - The right child of a node at position
nis at position2n + 1. - The parent of a node at position
nis at positionn/2.
Self-test: ArrayBST Representation
Here is an ArrayBST.
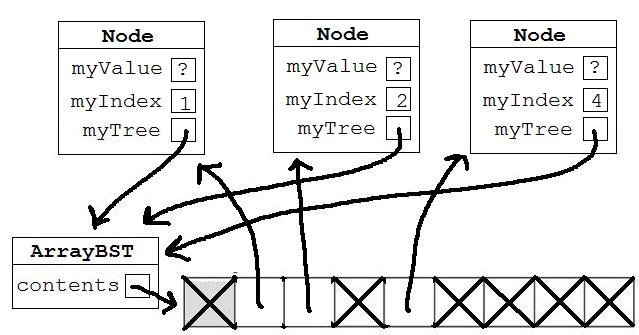
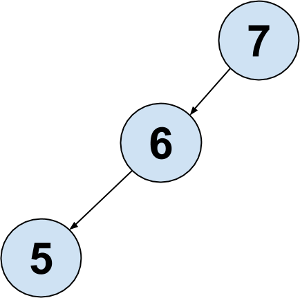
Which of the following trees could be represented by the ArrayBST shown above? (The myValues have been omitted and replaced with ?s)
Option 1
Option 2
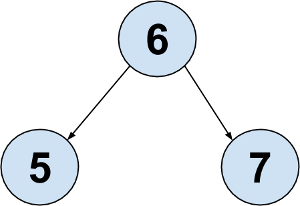
Option 3
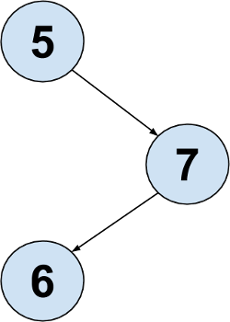
Option 4
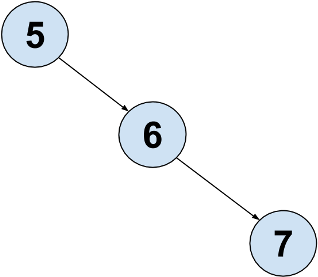
Choose one answer.
|
Option 1
|
Correct! The
ArrayBST
suggests there is a root with one left child and no right child, and the left child has a left child.
|
|
|
Option 2
|
Incorrect. The
ArrayBST
shows the root has no right child.
|
|
|
Option 3
|
Incorrect. The
ArrayBST
shows the root has no right child.
|
|
|
Option 4
|
Incorrect. The
ArrayBST
shows the root has no right child.
|
Now we have a new ArrayBST:
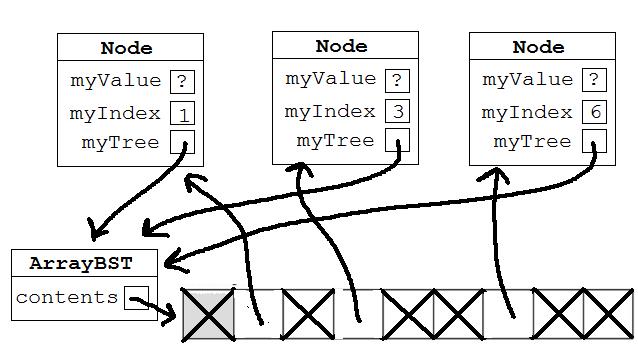
Which of the trees could represent it? Choose one answer.
|
Option 1
|
Incorrect. The
ArrayBST
shows the root has no left child.
|
|
|
Option 2
|
Incorrect. The
ArrayBST
shows the root has no left child.
|
|
|
Option 3
|
Correct! The
ArrayBST
shows the root has a right child which has a left child.
|
|
|
Option 4
|
Incorrect. Because there is nothing in position 7, the right child of the root can't have a right child.
|
Now suppose we have this ArrayBST:
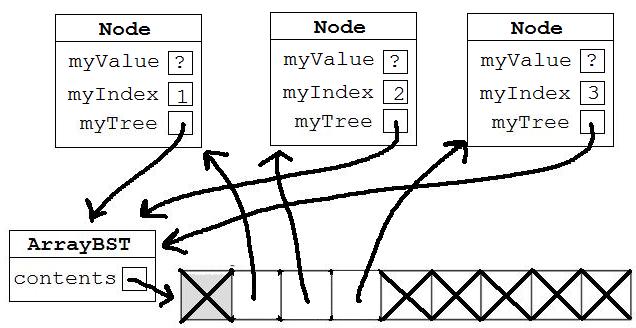
|
Option 1
|
Incorrect. The
ArrayBST
shows that the root has a right child.
|
|
|
Option 2
|
Correct! The
ArrayBST
shows that the root has both a left and right child.
|
|
|
Option 3
|
Incorrect. The
ArrayBST
shows that the root has a left child.
|
|
|
Option 4
|
Incorrect. The
ArrayBST
shows that the root has a left child.
|
Exercise: Implement ArrayBST
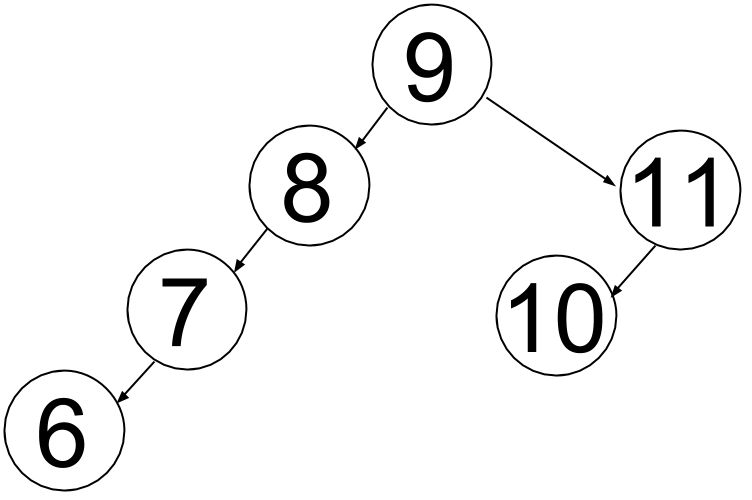
Download the framework code at ArrayBST.java, or listed below. Fill in the methods getLeft, getRight, getParent, setLeft, and setRight being sure not to violate the layers of abstraction (use the setNode method we implemented!) Check that the main method creates the tree shown below.
Self-test: a Naive BST contains
Code for the contains method appears below. Complete the following statement:
public boolean contains (int value) {
for (Node treeNode : contents) {
if (treeNode != null && treeNode.myValue == value) {
return true;
}
}
return false;The contains method runs in time proportional to in the worst case.
|
h, the height of the tree
|
Incorrect. This would be true if we searched through our tree smartly, but not using the naive algorithm shown above.
|
|
|
n, the number of nodes in the tree
|
Incorrect. We iterate through
contents
. Is everything in
contents
the number of nodes in the tree?
|
|
|
l, the length of the array that contains the tree
|
Correct! Notice that we iterate through positions in the array that might not even contain nodes.
|
Exercise: Rewrite contains
Rewrite the contains method in ArrayBST.java to run in time proportional to the height of the tree. Make sure to keep with the abstraction (use the getLeft and getRight you wrote!). Augment the main method with simple checks to make sure your contains works.
C. Implementations of queues and priority queues
Queues and Priority Queues
Earlier in the class we looked at queues, a data structure that keeps items in order. Remember they process items in a first-in-first-out system.
Sometimes, however, processing items in the order they arrive is not what we want to do. We may instead want to process items in order of importance or a priority score. Enter the priority queue...
Queues and priority queues have the same operations:
- construct an empty queue
- enqueue: add an element somewhere in the queue
- dequeue: remove an element from the queue (for a normal queue, this is the oldest element in the queue. For a priority queue, this is the one with most priority)
- isEmpty: check if the queue is empty
- peek: get the item at the front of the queue without removing it
Traditionally, Black Friday lines are like a queue...

People are served based on the order they arrive, regardless of what they want to buy.
An emergency room is like a priority queue...

The people waiting with the most pain are served first, regardless of when they arrived.
Why this is important: Priority queues are an integral component of many algorithms for graph processing (which we'll cover in a few labs). For example, the first few weeks of CS 170 typically involve graph algorithms that use priority queues. Look out for priority queues in other CS classes as well — for example, you'll find them invaluable the operating systems class CS 162, where they're used to schedule which processes in a computer to run at what times.
Self-test: Runtimes of Different Priority Queue Implementations
For the following examples, we will follow Java's default priority for a priority queue, which prioritizes items with the smallest value first (assuming the items are Comparable). Note that you can create a priority queue with your own custom priority by using the following priority queue constructor: PriorityQueue(int initialCapacity, Comparator<? super E> comparator).
Consider the implementation of a priority queue with an unordered linked list of N elements, and complete the following sentence:
- In the worst case, the run time to insert something into the priority queue is proportional to .
|
n
|
Incorrect. The linked list is unordered, so we can put it anywhere, and faster than this.
|
|
|
log n
|
Incorrect.
|
|
|
constant
|
Correct! We can just attach it to the front of the linked list.
|
|
|
n^2
|
Incorrect.
|
|
|
n log n
|
Incorrect.
|
Consider the implementation of a priority queue with an unordered linked list of N elements, and complete the following sentence:
- In the worst case, the run time to remove the element with highest priority is proportional to .
|
n
|
Correct! We search through every item in the linked list until we find it. Then removal happens in constant time.
|
|
|
n log n
|
Incorrect.
|
|
|
constant
|
Incorrect. The linked list is unordered, so in order to find the element with higher priority we have to search for it in the linked list.
|
|
|
n^2
|
Incorrect. Remember once we find an item in a linked list, we can remove it in constant time.
|
|
|
log n
|
Incorrect.
|
Consider the implementation of a priority queue with an ordered linked list of N elements, and complete the following sentence:
- In the worst case, the run time to insert something into the priority queue is proportional to .
|
n^2
|
Incorrect.
|
|
|
log n
|
Incorrect.
|
|
|
constant
|
Incorrect. Since the list is ordered, we first have to find the correct spot to insert it.
|
|
|
n log n
|
Incorrect.
|
|
|
n
|
Correct! We have to search for the correct spot to insert the node, since the list is order.
|
Consider the implementation of a priority queue with an ordered linked list of N elements, and complete the following sentence:
- In the worst case, the run time to remove the element with highest priority is proportional to .
|
n
|
Incorrect. The list is already ordered, so finding the element with highest priority is easy.
|
|
|
n log n
|
Incorrect. The list is already ordered, so finding the element with highest priority is easy.
|
|
|
constant
|
Correct! The list is already ordered, so we just have to get the item at the front of the list.
|
|
|
log n
|
Incorrect.
|
|
|
n^2
|
Incorrect.
|
Consider the implementation of a priority queue with a balanced binary search tree of N elements, and complete the following sentence:
- In the worst case, the run time to insert something into the priority queue is proportional to .
|
log n
|
Correct! The tree is balanced and we may have to to travel all the way down its height to insert.
|
|
|
n
|
Incorrect. The tree is balanced so we don't have to worry about traversing all nodes in the worst case.
|
|
|
n^2
|
Incorrect.
|
|
|
constant
|
Incorrect. When we insert into a BST, we have to traverse the tree to find the correct place to insert it.
|
|
|
n log n
|
Incorrect.
|
Consider the implementation of a priority queue with a balanced binary search tree of N elements, and complete the following sentence:
- In the worst case, the run time to remove the element with highest priority is proportional to .
|
log n
|
Correct! We have to search all the way down the left branch of the BST to find the smallest element.
|
|
|
n^2
|
Incorrect.
|
|
|
n
|
Incorrect. The binary tree is balanced so we don't have to worry about the worst case of search every node.
|
|
|
n log n
|
Incorrect.
|
|
|
constant
|
Incorrect. Remember the highest node in a BST isn't at an accessible location (it isn't the root). It's all the way down the left branch of the tree.
|
Queue and PriorityQueue in java.util
The java.util library contains a Queue interface and a PriorityQueue class that implements Queue. Queue methods include the following:
offer(element), which adds the element to the queue (this is enqueue)peek(), which returns but does not remove the head of the queuepoll(), which retrieves and removes the head of the queue (returning null if the queue is empty) (this is dequeue)
Java's priority queue is implemented with a data structure called a binary min heap. In the rest of this lab you will study and implement this data structure yourself.
Binary Heaps Intro
Having a fast implementation of a priority queue would be very helpful, but as we saw in the last self-test, the most obvious implementations each have flaws. Enter the binary heap. The binary heap is a data structure that will help us implement a priority queue with fast operations. This means we want to be able to quickly insert objects into the heap with different priority values, and we want to be able to quickly remove the most important item quickly.
There are two flavors of binary heaps: min heaps and max heaps. They're very similar except the former organizes items with the smallest given the most importance, and the latter organizes items with the largest given the most importance. Choose either one depending on what your definition of a priority score is.
In these labs we may work with either a max or min heap. It should be easy to figure out how the other one works by example. But pay attention so you don't get confused which one we're using!
D. Work with binary heaps
Binary Heaps Defined
Binary min heaps are basically just binary trees (but not binary search trees) — they have all of the same invariants of binary trees — with two extra invariants:
- Invariant 1: the tree must be maximally balanced (more on this later)
- Invariant 2: every node is smaller than its descendents (there is another variation called a binary max heap where the reverse is true)
Invariant 2 guarantees that the min element will always be at the root of the tree. This helps us access that item quickly, which is what we need for a priority queue.
We need to make sure binary heap methods maintain the above two invariants. Here's how we do it:
Add an item
- Put the item you're adding in the next available spot in the bottom row
- Swap the item you just added with its parent until it is larger than its parent, or until it is the new root. This is called bubbling up.
Remove the min item
- Replace the item at the root with the item in the last bottom spot
- Bubble down the new root until it is smaller than both its children. If you reach a point where you can either bubble down through the left or right child, you must choose the smaller of the two.
Maximally Balanced Trees
There are a couple different notions of what it means for a tree to be well balanced. A binary heap must always be what is called maximally balanced (also sometimes called complete).
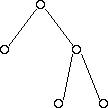
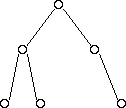
A maximally balanced tree:
- Has all available positions for nodes filled, except for possibly the last row, which must be filled left-to-right
Below are some examples of trees that are maximally balanced:
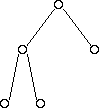
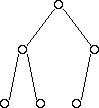
And some examples of trees that are NOT balanced:
Play with Heaps
We just covered a lot of new concepts for heaps. To test yourself and see if you understand them, try drawing a heap. Draw what happens when you insert numbers into the heap and when you decide to remove the smallest (or biggest) one.
Also, check out this interactive animation of a min heap. You can type in numbers to insert, or remove the min element (ignore the BuildHeap button for now; we'll talk about that shortly). You can use this animation to check your own drawings too — there is no ambiguity when constructing heaps, so if you insert numbers in the same order, yours should look exactly the same as this animation.
Exercise: Writing Heap Methods
First, switch which partner is coding for this lab, if you haven't recently.
The class ArrayHeap implements a binary max heap using an ArrayList (just like ArrayBST implemented a BST). Fill in the missing methods in ArrayHeap.java.
Respect the abstraction! — insert, removeMin, and changePriority may use the methods bubbleUp and bubbleDown. bubbleUp and bubbleDown may use getLeft, getRight, and getParent (which should be the same as what you wrote for ArrayBST).
E. Binary heap brainteasers
Self-test: Heaps and BSTs
Consider binary trees that are both max heaps and binary search trees.
How many nodes can such a tree have? Check all that apply.
|
0 nodes
|
Correct! A 0-node tree is trivially both a BST and a max heap.
|
|
|
1 node
|
Correct! A 1-node tree is trivially both a BST and a max heap.
|
|
|
2 nodes
|
Correct! A root node could have a left child and still be both a BST and a max heap.
|
|
|
3 nodes
|
Incorrect. The heap will have both a left and right child to satisfy the heap shape requirement. But then the root must be the highest element for the heap, and the middle element for the BST.
|
|
|
4 nodes
|
Incorrect. Follows from 3.
|
|
|
5 nodes
|
Incorrect. Follows from 3.
|
|
|
Any number of nodes
|
Incorrect. Follows from 3.
|
|
|
No trees exist
|
Incorrect. Consider the simple cases.
|
Self-test: Determining if a Tree is Maximally Balanced
It's not obvious how to verify that a linked binary tree is maximally balanced (aka complete). A CS 61B student suggests the following recursive algorithm:
- A one-node tree is complete.
- A tree with two or more nodes is complete if its left subtree is complete and has depth k for some k, and its right subtree is complete and has depth k or k-1
Here are some example trees. Think about whether or not the student's proposed algorithm works correctly on them.
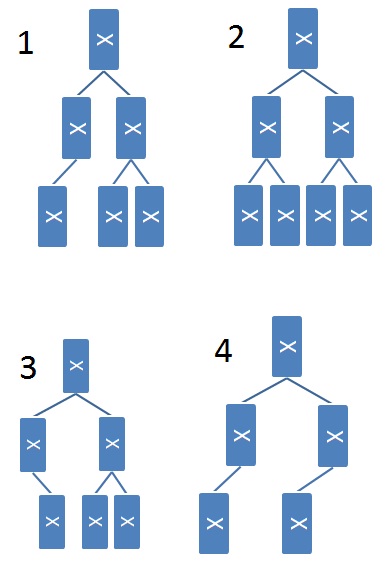
Check all that apply to test your understanding of the proposed algorithm.
|
Tree 1 is maximally balanced
|
Incorrect. Remember a maximally balanced tree must fill the bottom row left-to-right
|
|
|
Tree 1 would be identified as maximally balanced
|
Correct! The student's algorithm makes a mistake in this case. The recursive algorithm doesn't propagate up correctly.
|
|
|
Tree 2 is maximally balanced
|
Correct!
|
|
|
Tree 2 would be identified as maximally balanced
|
Correct!
|
|
|
Tree 3 is maximally balanced
|
Incorrect. Remember a maximally balanced tree must fill the bottom row left-to-right
|
|
|
Tree 3 would be identified as maximally balanced
|
Incorrect. The algorithm will find a left subtree with depth 0 and compare it to a right subtree with depth 1, which will cause it to return false.
|
|
|
Tree 4 is maximally balanced
|
Incorrect. Remember a maximally balanced tree must fill the bottom row left-to-right
|
|
|
Tree 4 would be identified as maximally balanced
|
Correct. The student's algorithm makes a mistake here. The recursive algorithm doesn't propagate up correctly.
|
Discussion: Complete Trees and BFS
Link to the discussionAnother CS 61B student claims that a binary tree is complete if all the leaves in the tree come at the end of a breadth-first traversal of the tree. Give a counterexample to this claim.
Self-test: The Third Biggest Element in a Max Heap
Here's an example heap.
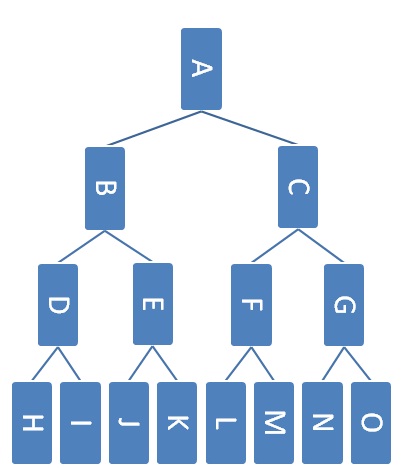
Which nodes could contain the third largest elements in the heap assuming that the heap does not contain any duplicates?
|
Node A
|
Incorrect. The top node must be the greatest node.
|
|
|
Node B
|
Correct! There may be the order A -> C -> B
|
|
|
Node C
|
Correct! There may be the order A -> B -> C
|
|
|
Node D
|
Correct! There may be the order A -> B -> D
|
|
|
Node E
|
Correct! There may be the order A -> B -> E
|
|
|
Node F
|
Correct! There may be the order A -> C -> F
|
|
|
Node G
|
Correct! There may be the order A -> C -> G
|
|
|
Node H
|
Incorrect. It has three nodes above it, all of which must be greater.
|
|
|
Node I
|
Incorrect. It has three nodes above it, all of which must be greater.
|
|
|
Node J
|
Incorrect. It has three nodes above it, all of which must be greater.
|
|
|
Node K
|
Incorrect. It has three nodes above it, all of which must be greater.
|
|
|
Node L
|
Incorrect. It has three nodes above it, all of which must be greater.
|
|
|
Node M
|
Incorrect. It has three nodes above it, all of which must be greater.
|
|
|
Node N
|
Incorrect. It has three nodes above it, all of which must be greater.
|
|
|
Node O
|
Incorrect. It has three nodes above it, all of which must be greater.
|
Which nodes could contain the third largest elements in the heap assuming that the heap can contain any duplicates? (NOTE: Heaps CAN contain duplicates)
|
Node A
|
Incorrect. The top node must be the greatest node.
|
|
|
Node B
|
Correct!
|
|
|
Node C
|
Correct!
|
|
|
Node D
|
Correct!
|
|
|
Node E
|
Correct!
|
|
|
Node F
|
Correct!
|
|
|
Node G
|
Correct!
|
|
|
Node H
|
Correct!
|
|
|
Node I
|
Correct!
|
|
|
Node J
|
Correct!
|
|
|
Node K
|
Correct!
|
|
|
Node L
|
Correct!
|
|
|
Node M
|
Correct!
|
|
|
Node N
|
Correct!
|
|
|
Node O
|
Correct!
|
F. Heapsort
Sort Some Numbers Using a Heap
The main method of ArrayHeap.java adds some numbers to a heap. Add code to the main method to print these numbers out from smallest to largest. It is fine if this modifies the heap in the process.
Notice we have just sorted the numbers!
Heapsort
Suppose you have an array of N numbers that you want to sort smallest-to-largest. As we saw in the last slide, one algorithm for doing this as as follows:
- Put all of the numbers in a min heap
- Repeatedly remove the min element from the heap, and store them in an array in that order
This is called heapsort.
Since each insertion takes proprotional to log N comparisons once the heap gets large enough, and each removal may also take proportional to log N comparisons, the whole process takes proportional to N log N comparisons.
It turns out we can actually make step 1 of heapsort run faster — propotional to N comparisons — using a process called heapify, which we'll cover on the next slide. (Unfortunately, we can't make step 2. run any faster than N log N, so the overall heapsort must take N log N time.)
Heapify
The algorithm for taking an arbitrary array and making it into a min (or max) heap in time proprotional to N is called heapify. Pseudocode for this algorithm is below:
def heapify(array):
index = N/2
while index < 0:
bubble down item at index
index--Conceptually, you can think of this as building a heap from the bottom up. To get a visualization of this algorithm working, click on the BuildHeap button on the animation we linked earlier. This loads a pre-set array and then runs heapify on it.
It is probably not immediately clear to you why this heapify runs in O(N). Don't worry about it — the math required for explaining it is beyond what you are expected to use in this course. For those who are curious, you can check out an explanation on Wikipedia here.
Finding the K Largest Elements
In the following problem you will reason about an algorithm that collects the K largest elements in a list of length N. Before you look at the questions, try to design an algorithm that could accomplish this in the asymptotically lowest amount of time.
What data structure would you use?
Self-test: Finding the K Largest Elements
You have N elements and you want to collect the K largest. You can use a heap to solve this problem. How large of a heap would you need? Choose one answer.
|
You need a heap of size K
|
Correct! We'll maintain a heap of the top k elements we've found so far.
|
|
|
You need a heap of size log N
|
Incorrect.
|
|
|
You need a heap of size N
|
Incorrect. While an algorithm using this could work, it wouldn't be the most efficient. Try to think of another approach.
|
What type of heap would be best to use? Choose one answer.
|
Max Heap
|
Incorrect. If you got this wrong, try drawing out the algorithm using a min heap and see how it works.
|
|
|
Min Heap
|
Correct! We want quick access to the smallest of the top k elements we've found so far. That way, we can replace it easily if we find something bigger.
|
What would the run-time be proportional to for this algorithm? Choose one answer.
|
N log K
|
Correct! We'll end up adding all N elements to our heap of size K. Each insertion of an element will take log K time.
|
|
|
N
|
Incorrect.
|
|
|
K log N
|
Incorrect.
|
|
|
K log K
|
Incorrect.
|
|
|
N log N
|
Incorrect.
|
This is a tricky algorithm! If you still can't picture how it works, draw out the heap, add all the list elements to it, and see what happens.
G. Conclusion
Submission
IMPORTANT!: Before this lab is due, please fill out an evaluation on your group members' performances for project 2. You can find it here. This is to be done individually. You will get 0 points on the project if you do not fill it out, so please don't forget. Thanks!
Submit the following files as lab19.
- ArrayBST.java
- ArrayHeap.java
Reading
For next lab, read DSA chapter 13.1 - 13.4 (Graphs).