A. Intro
Download the code for Lab 11 and create a new Eclipse project out of it.
Learning Goals for Today
Today you will work with a third way to represent a linked list, one that uses a wrapper class. In general, a wrapper class is any class that "wraps" or "encapsulates" the functionality of another class or component. The wrapper class provides a level of abstraction from the implementation of the underlying class or component. In this lab, the wrapped objects are ListNodes; the wrapper is a List. A user only calls methods on the List, leaving all the operations on ListNodes to happen below the abstraction barrier.
You'll be rewriting methods coded earlier to use the new representation.
B. List wrapper class
Another Way to Represent a List
In the previous two labs, we worked with an implementation of a linked list that used three classes: An AbstractListNode, a NonemptyListNode and an EmptyListNode. An example of that implementation is shown below.
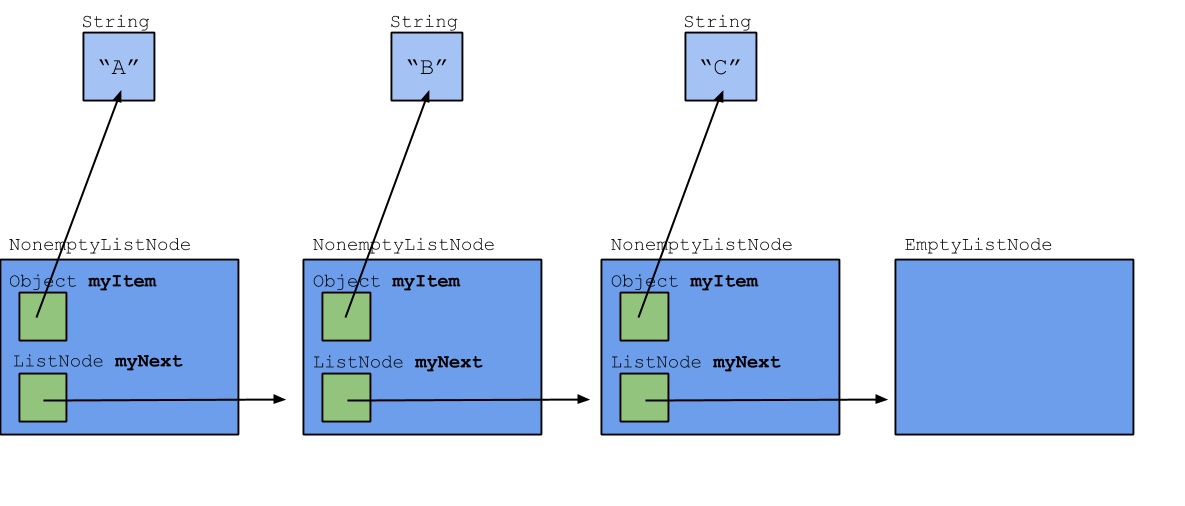
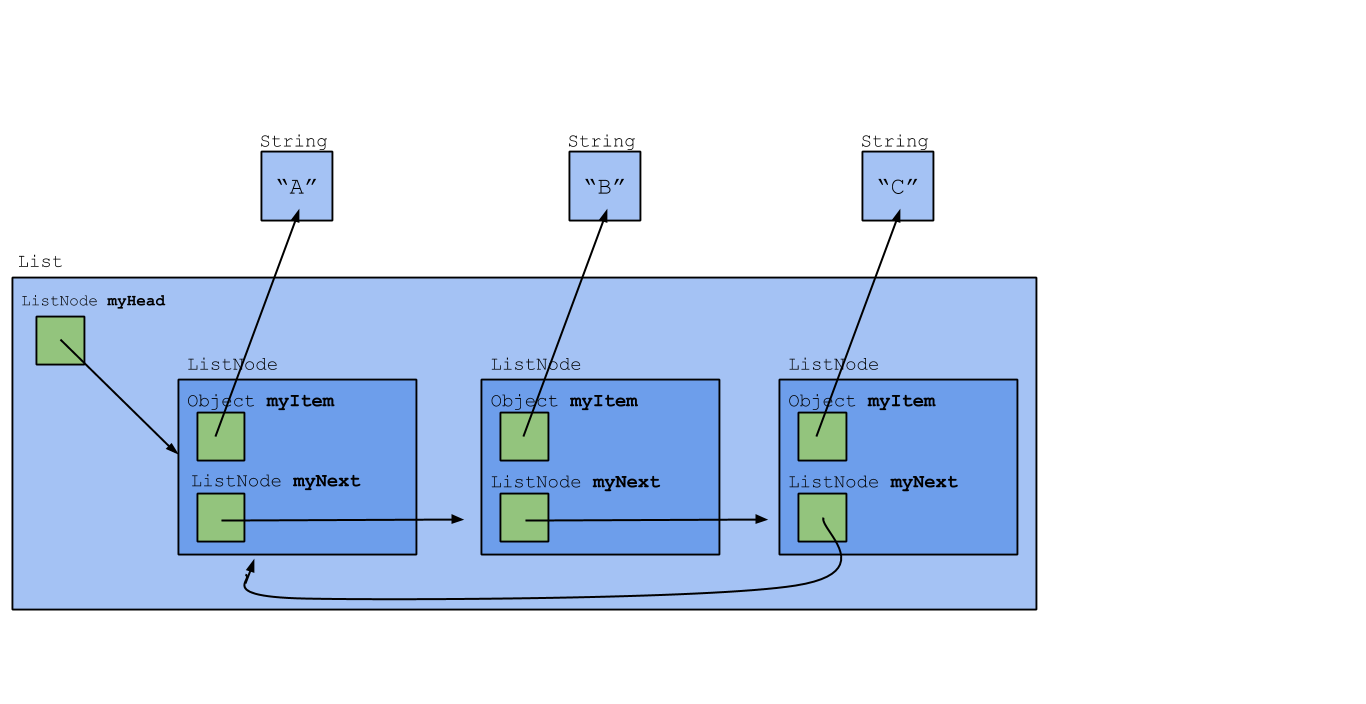
In this lab, we'll look at a different implementation of a linked list. In this implementation, we'll only use one type of list node, ListNode. However, we'll also use another class, List, which represents the whole list. A List object will still exist even if the list is empty and there are no nodes; this is why we won't need a special EmptyListNode class. A drawing of this implementation is shown below.
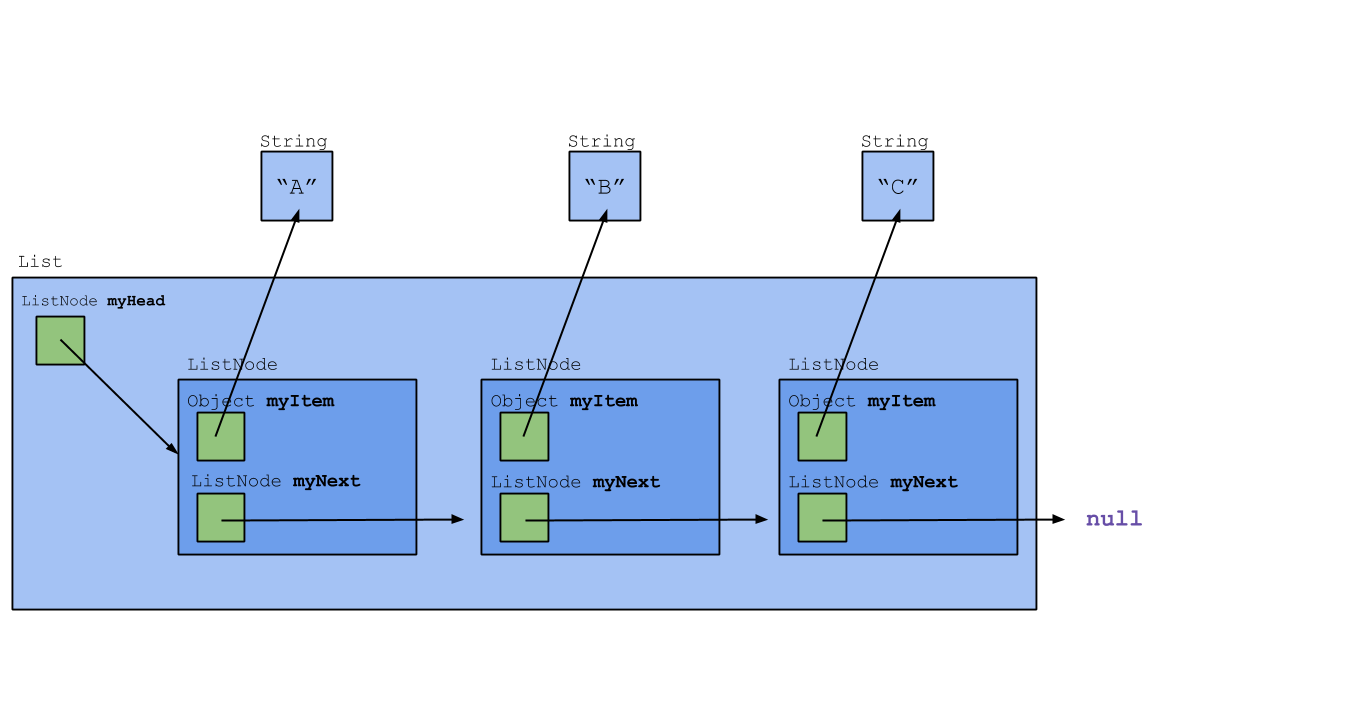
(We may have told you before not to draw objects inside other objects, yet the ListNode object here appears inside List. Why? Because ListNode is a private nested class of List, and ListNode objects cannot exist or be accessed out of List. For that reason, we draw them inside.)
A Wrapper Class Protects List Integrity
It's clear, we hope, that allowing any method to call setNext to change the links in a list invites disaster.
The solution is to wrap the ListNode class inside another class, which we'll call List. The List class will have a ListNode instance variable—we'll call it myHead—that refers to the first node in the linked list. Here's an outline of the class:
public class List {
private ListNode myHead;
public List() {
myHead = a representation of an empty list;
}
// note this is a private class of List
private static class ListNode {
private Object myItem;
private ListNode myNext;
...
}
...
}The List class will provide most of the methods previously provided by the ListNode class, but access to myItem and myNext will not be allowed outside of the List class.
Normally, one must have an instance of the outer class in order to instantiate a nested class. The ListNode class is declared as static because there are occasions where we will want to (briefly) create a ListNode object that's not connected to any List object.
Some Code for the List Class
We've provided some code for the new List class to save you some of the trouble of reimplementing this new type of linked list. Check it out below. You can also find it in List.java. The file ListTest.java contains a JUnit test suite.
Looking below, you may observe that more of the methods are iterative as opposed to recursive. Many fit the following pattern:
for (ListNode p = myHead; p != null; p = p.myNext) ...You'll find this pattern useful yourself.
Exercise: The equals Method
Write the equals method, which determines if this list contains the same elements in the same sequence as the argument list. The JUnit test suite contains a test method.
Exercise: The add and appendInPlace Methods
Write the add method, which adds its argument as the last element of this list. For instance, if this list contains the elements "a", "b", and "c", then the result of adding "d" is the list containing the elements "a", "b", "c", and "d", in that order. Make the method destructive. Don't return a new list; modify the existing one.
Then, write the appendInPlace method (it will be similar in structure to add). Make this method destructive. Don't create any new nodes.
The JUnit test suite contains tests for both these methods.
Exercise: Iterator Methods
If you haven't yet switched which partner is coding in this lab, do so now.
Make List implement Iterable. Framework code is below, which should go inside of the List class. Like the ListNode class, the ElementIterator class is within the List class. However, this one is not static, and you can only create an instance of the inner class ElementIterator if you already have a List object. As a consequence, inside of the ElementIterator class you can access an instance variable myHead and call methods from the ListNode class. Make sure to import java.util.*;. There is a test method in the JUnit file.
public Iterator iterator() {
return new ElementIterator();
}
public class ElementIterator implements Iterator {
// State variable(s) to be provided.
public ElementIterator() {
// TODO code to be provided
}
public boolean hasNext() {
return false;
// TODO code to be provided
}
public Object next() {
return null;
// TODO code to be provided
}
public void remove() {
// not used; do not implement
}
}Exercise: Opportunities for Efficiency
A principle of organizing data for efficient access is the following:
- If you need to access information quickly, store it (or a reference to it) somewhere.
The List class provides an opportunity to apply this principle. In particular, both add and appendInPlace currently search for the last node in the list, and size does essentially the same thing to count the nodes in the list. To save time, we can provide two more instance variables: an int named mySize will store the length of this list, and a ListNode named myTail, will store a reference to the last node in this list. (Both myHead and myTail will contain null if this list is empty. Both will point to the same node if there is only one node in the list.)
Modify the size, add, addToFront, and appendInPlace methods to accommodate these two new variables. The ListTest.java tests should still be appropriate tests for your modifications.
Exercise: A Consistency Checker
Write a List method named isOK that checks this list for consistency. In particular, it should check that
- the value stored in
mySizeis the number of nodes in this list - all
myItemobjects in this list are non-null - either both
myHeadandmyTailare null, ormyTailis a reference to the last node in the list whose first node is the node thatmyHeadrefers to.
(These are data invariants.)
The isOK method does the clear-box testing that's not possible with JUnit.
Exercise: A remove Method
Write and test a List method named remove that, given an Object as argument, removes all elements that are equal to that object from the list. The method should be destructive, modifying the existing list rather than returning a new one.
C. More mutation exercises
Duplicating Each Node in a Linked List
Fill in the body of the loop in the List method doubleInPlace, whose framework is given below. Each node in the list should be copied in place, resulting in a list that's twice as long. For example, if the list initially contains (a b c), it should contain (a a b b c c) after the call to doubleInPlace. This is a destructive method.
Don't call any methods other than the ListNode constructor, and don't call it more than once per node in the original list.
Here's the framework.
public void doubleInPlace() {
for (ListNode p = myHead; p != null; p = p.myNext) {
// TODO Your code here
}
// TODO And maybe here as well
}Reversing a List
Over the next few steps, we're going to be working on a method to reverse a List using our current List implementation.
- We will assume the restriction that the reversal is to be done in place, that is, without creating any new
ListNodes. - As noted in an earlier lab session, a static method will be helpful.
- We must pay close attention to the
myNextreferences when we reverse all of the links.
Reversing a List in Place
To reverse the list in place, we recommend using a static helper method.
Here's the framework code for reverse. Don't fill it in yet.
public void reverse() {
// ...
}
public static void reverseHelper(ListNode l, ListNode soFar) {
// ...
}An Invariant for Reversing a List
This framework suggests we maintain a recursion invariant that relates the values of L and soFar at each call.
Here is a trace of a call to reverse with the list that represents {A, B, C, D}
| Method called | L | soFar |
|---|---|---|
| reverse | {A, B, C, D} | N/A |
| reverseHelper | {A, B, C, D} | {} |
| reverseHelper | {B, C, D} | {A} |
| reverseHelper | {C, D} | {B, A} |
| reverseHelper | {D} | {C, B, A} |
| reverseHelper | {} | {D, C, B, A} |
Discussion: An Invariant for reverse
Link to the discussionWork with your partner to identify the invariant between the reverseHelper arguments L and soFar that is true at each call to reverseHelper.
Exercise: Completing the reverse Method
First, if you haven't switch which partner is coding recently, do so now.
Whenever helper is called, L is the list of elements not yet reversed, and soFar is the reversed list of the elements already processed. To design the procedure from this relation, we position ourselves in the middle of the recursion, say, with L equal to (C D) and soFar equal to (B A). What do we do with C, the next element in L, so that soFar is the reverse of (A B C)? The answer is to add it to the current soFar.
We apply the same reasoning for the reverseHelper method. Here's its header:
private static ListNode reverseHelper(ListNode l, ListNode soFar) {
if (l == null) {
return soFar;
} else {
...
}
}Again, we position ourselves in the middle of the recursion. For design in Java, it helps to draw box-and-arrow diagrams; here's the situation with L pointing to the list (C D) and soFar pointing to the list (A B), along with the structure that should be passed to the recursive call. The boxes outlined in bold are the boxes whose contents should change.
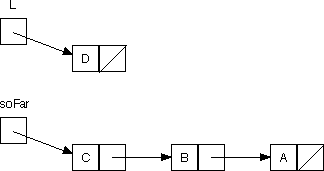
There are three changes to be made. All are interdependent, though, so we need a temporary variable:
ListNode temp = l.myNext;
l.myNext = soFar;
return reverseHelper ( ____ , ____ );The copying of the arguments in the recursive call will provide the other two changes to box values.
Fill in the arguments of the recursive call to complete the method. Then try it out with a JUnit test.
Exercise: An Iterative Reverse
Fill in the framework for reverseHelper (given below) so that, instead of making a recursive call, it uses a loop to change the relevant links. (You'll also need to change the call to reverseHelper.) Each iteration of your loop should maintain the invariant described for the recursive version. Your JUnit test from the previous step should work for this version as well.
Here's the framework.
private static ListNode reverseHelper(ListNode head) {
ListNode p, soFar;
// p plays the role of l in the previous version.
for (p = head, soFar = null; p != null;) {
ListNode temp = p;
...
}
return soFar;
}D. Variations on linked lists
Linked List Variations
You've seen three ways to implement a linked list so far: a simple barebones implementation, an implementation that uses AbstractListNode, and an implementation that has a List class. Here are three more possible variations.
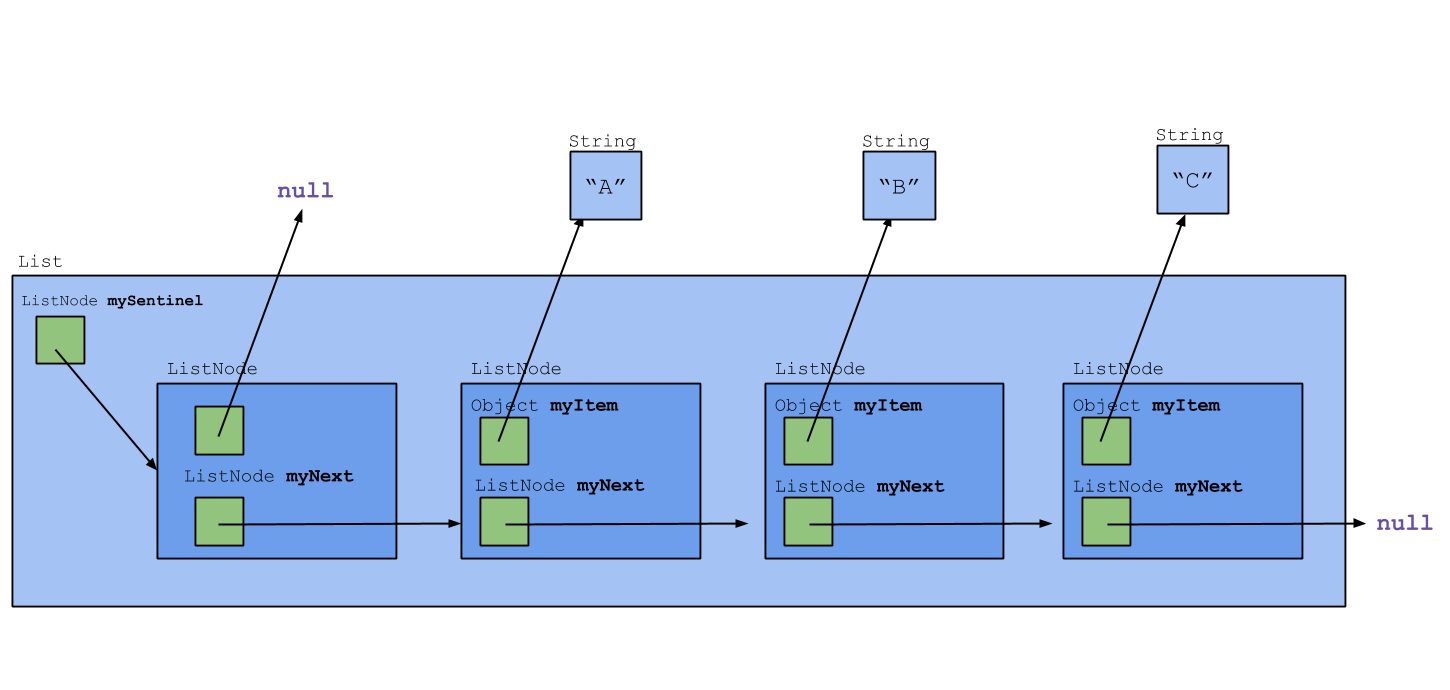
Sentinel list variation
Circular list variation
Doubly linked variation
Sentinel List Variation
This is very similar to the abstract implementation from earlier, just with an empty node at the front rather than at the end, and named a little differently. Why use this?
In coding some of the List methods, you may have noticed a bit of awkwardness arising from the need to handle a modification to the start of the list differently from a modification anywhere else:
if (myHead == null) {
// update myHead
} else {
// update some myNext field
}This awkwardness can be eliminated if we guarantee that there will always be at least one node in the list. We did this in our first list representation; there, every list ended with an EmptyListNode. Here, we can ensure this condition by including a dummy header node as the first element in the list. In most circumstances, its myItem value is ignored. (When the list elements are to be maintained in sorted order, the myItem value would be the smallest or largest representable value.) Iterator code would have to be revised to skip the dummy node, so we trade off one area of clumsiness for another.

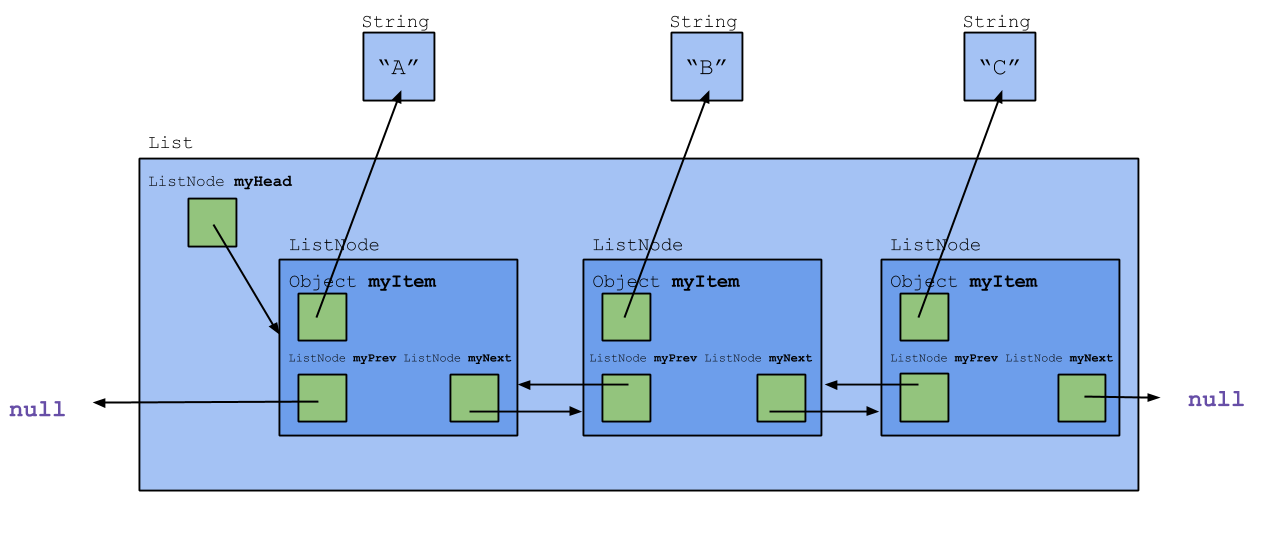
Doubly Linked Lists
Another bit of awkwardness in list processing arises when inserting or deleting a list element. In these situations, the myNext variable in the ListNode object immediately prior to the node being inserted or deleted must be changed.
A way to deal with this is to use a doubly linked list. Each node in the list contains not only a reference to the next node but also a reference to the immediately preceding node, as shown in the following diagram.
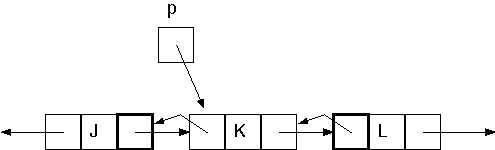
To delete a node, we need only a reference to the node being removed. The diagram below displays a situation where the node referred to by p is to be removed. The parts of the neighboring nodes that must change to do the removal are highlighted in boldface. One may note that each changing node part can be accessed through p.

Circular Lists
Occasionally we find it useful to have the last node in a list point back to the first node, thus creating a circular structure. (You created such a structure in an earlier activity.) One obviously needs to worry about infinite loops with such a structure, so processing involves saving a reference to a node in the list and then comparing it with an iteration reference to make sure we don't go past the end of the list.

Exercise: Managing a Circular Doubly-linked List
The code Sequence.java, is an incomplete class that represents a sequence as a circular doubly-linked list. You are to supply the code for the delete method and the Iterator methods. Comment out the existing body of toString and comment in the alternative implementation to test the Iterator code.
Hint: You will probably need additional state information in the SequenceIterator class beyond a DListNode variable, so that your hasNext method will perform correctly. We suggest a counter or a boolean returnedFirstItem variable.
E. Experiment with java.util
Exercise: Timing Experiments with java.util Classes
You already know about the ArrayList class. The java.util library also contains a LinkedList class. They both implement the Interface List shown here
In the next couple of steps, you'll perform some timing experiments that investigate properties of these two classes. Each experiment should involve only one or two timings (to find an n big enough to show a difference), along with some big-Oh analysis. You may use the Timer class used earlier with sorting methods (it's in the lab folder as Timer.java).
Submit your explanations with the rest of the lab.
Experiment 1
Using only methods common to both ArrayList and LinkedList, design an experiment to show performance differences between the two List implementations.
Experiment 2
The online documenation for Java's LinkedList claims that it's implemented as a doubly-linked list. Design an experiment that supports this claim. In particular, your experiment should show that the underlying implementation is not a singly-linked list with a head and tail pointer.
For today's lab, please write up the results of your timings from the step "Timing experiments for java.util classes".
In particular, answer the following questions:
- Describe your experiment 1 and its results, and explain why it distinguishes between an
ArrayListand aLinkedList. - Describe your experiment 2 and its results, and explain why it distinguishes between a doubly linked list and a singly linked list with head and tail pointers.
Provide enough information so that another CS 61 BL student could duplicate your tests and verify your results. Answers to the questions and relevant code should be submitted in a file called Timing.txt.
F. Conclusion
Summary
We encountered several linked representations for a sequence of values over the past three labs.
- The first approach was to represent all the values in the sequence with
ListNodes, each storing a sequence value and a reference (pointer). The reference is to theListNodestoring the next value in the sequence. A problem is that in this representation, there's no way to represent an empty sequence. - To fix this, we created an
EmptyListNodeclass and renamed theListNodeclass toNonemptyListNode. Both have the same set of methods (though obviously not the same set of behaviors), suggesting that they both inherit from an abstract class. Using this representation, we implemented several list operations. - There was still the problem of insufficient information hiding. If any
ListNodeobject is accessible in the rest of the program, they all are, and a programmer might accidentally leave a value in an invalid state. The solution is to invent a second class,List, that contains a reference to the firstListNodein the sequence, the declaration ofListNode(now a nested class), and various methods that restrict the inspection and manipulations of the list information.
We then went on to examine three variations of the "standard" linked list, namely a circular list (which links its last node to its first node), a doubly linked list (in which each node contains a reference to its next node and its previous node, and a list with a "dummy" header node. Circular lists are models for circular processes, e.g. a scheduler of jobs running on a computer; a circular list is also good for implementing a queue (topic to come). Doubly linked lists allows inserting a value into or deleting it from the list without using a trailing pointer. A dummy header makes the check for an empty list unnecessary.
The activities mostly involve implementing list operations in up to three ways. We hope that this solidified your understanding of linked representations rather than bored you.
Submission
For this lab, the files to be submitted are:
- List.java
- Sequence.java
- Timing.txt
Submit these files as lab11.
Readings
The reading over the next two labs is DSA chapter 9 (Maps and Dictionaries).