A. Intro
Download the code for Lab 7 and create a new Eclipse project out of it.
Learning Goals for Today
Consider what happens when an error occurs, say, an out-of-bounds array access is made. The program may be allowed to crash. Java also, however, allows a programmer to intercept the crash and take alternate action. The mechanism that enables this ability is called an exception.
An exception can be thrown—passed to another part of the program to handle—or caught—handled on its own. We'll consider examples of each kind of use in the upcoming lab exercises.
After learning about exceptions, you'll learn about consistency checking, a new technique to help you debug.
B. Exceptions
Error Handling
So far in this course, we have not dealt much with error handling. You were allowed to assume that the arguments given to methods were formatted or structured appropriately. However, this is not always the case due to program bugs and incorrect user input:
- bugs in your programs might create inconsistent structures or erroneous method calls (e.g. division by zero, indexing out of bounds, dereferencing a null pointer)
- users cannot be trusted to give valid input (e.g. non-numeric input where a number is required or search failures where a command or keyword was misspelled)
We assume in the following discussion that we can detect the occurrence of an error and at least print an error message about it.
A big challenge in dealing with the error is to provide information about it at the right level of detail. For instance, consider the error of running off the end of an array or list. If the contents of a list are inconsistent with the number of elements supposedly contained in the list, a "reference through a null pointer" or "index out of bounds" error may result. The programmer may wish to pass information about the error back to the calling method with the hope that the caller can provide more appropriate and useful information about the root cause of the error and perhaps be able to deal with the error.
Here are some options for handling errors in this situation:
- Don't pass any information to the caller at all. Print an error message and halt the program.
- Detect the error and set some global error indicator to indicate its cause.
- Require the method where the error occurs as well as all methods that directly or indirectly call it, to pass back (or take back) an extra argument object that can be set to indicate the error.
All these options have flaws, which you will now discuss with your classmates.
Discussion: Comparison of Error-Handling Approaches
Link to the discussionHere are three approaches to error handling:
- Don't try to pass back any information to the caller at all. Just print an error message and halt the program.
- Detect the error and set some global error indicator to indicate its cause.
- Require the method where the error occurs, along with every method that, directly or indirectly, calls it, to pass back as its value or to take an extra argument object that can be set to indicate the error.
Which seems most reasonable? Defend your answer. If none, justify why all the options are bad.
Exceptions
There is a fourth option for handling errors, called an exception. Provided by Java and other modern programming languages, an exception signals that an error of some sort has occurred. Java allows both the signaling of an error and selective handling of the error. Methods called between the signaling method and the handling method need not be aware of the possibility of the error.
An exception is thrown by the code that detects the exceptional situation, and caught by the code that handles the problem. These two definitions are helpful in discussing exceptions.
When a method throws an exception, that exception must be dealt with by whatever method called exception method. That method can choose to either catch the exception and handle it, or it can choose to throw the exception again, passing it on to the method that called it.
Think of a hot potato. When a method generates an exception, it doesn't want to deal with it, so it throws the exception to the next method. That method must do something when it receives the exception. It can either handle it, or throw it to the next method. Methods keep throwing the exception until one is willing to catch it. If no methods end up catching an exception, then the Java program will look to to more drastic exception handlers, which may do things like exit the program and print a stack trace to the user. Before, we've called this behavior "crashing" the program.
There is a wide spectrum of "exceptional" situations. There may be catastrophic situations like the computer powering off. On the other hand, there are situations that might not even correspond to errors, like encountering the end of an input file. In between are errors varying in severity.
Exceptions in Java
Java's exception facility classifies all these into two categories:
- checked exceptions: exceptions that a method must explicitly handle or hand off to its caller
- unchecked exceptions: exceptions that a method need not worry about
The requirement for handling checked exceptions may encourage programmers into thinking about potential sources of error, with the result that more errors are detailed and handled correctly.
Exceptions are just Objects and are part of the regular class hierarchy as shown below.
All exceptions in Java are subclasses of the Exception class.
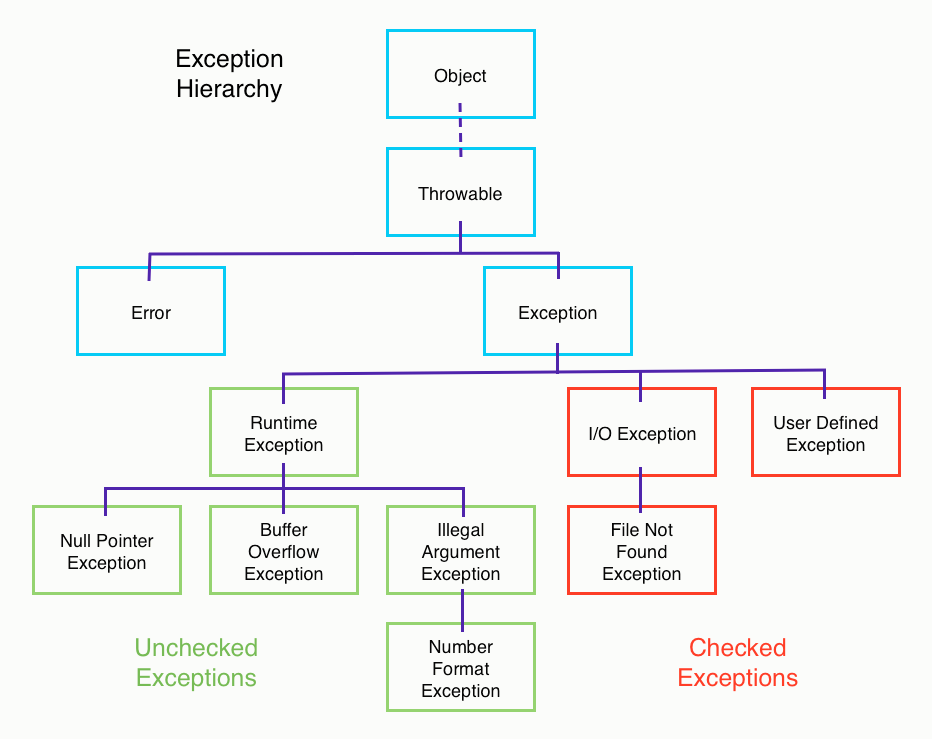
An exception is thrown when the exceptional event occurs. Normally, an exception stops the program. One may, however, choose to catch the exception and process it in such a way that the program can continue executing.
Catching Exceptions in Java
Catching an exception means handling whatever exceptional condition has arisen.
This is done by surrounding code that might produce exceptional conditions
with a try catch block as follows:
try {
// code that might produce the exception
} catch (exceptionName variableName) {
// code to handle the exceptional situation
}An example of where an exception is particularly useful is dealing with user
input. The AddingMachine program we saw in an earlier activity successively
read integers from the input. Users tend to be imperfect; they might mistype
the input. Thus, we need to be careful to make sure that they actually enter
a number to be added. The Scanner class helps with this as its nextInt
method throws an exception if the token being read isn't an integer.
Scanner intScan = new Scanner(System.in);
int k;
try {
k = intScan.nextInt ( );
} catch (NoSuchElementException e) {
// ran out of input
} catch (InputMismatchException e) {
// token isn't an integer
}Observe that the "tried" code can be simpler since it is coded as if nothing will go wrong. You can catch multiple exceptions, as in the code above, and handle them separately by supplying multiple catch blocks (ordered from most specific to least specific).
Generate Some Exceptions
Fill in the blanks in the code below (which is also in
TestExceptions.java) so that, when run, its output is:
/**
* Desired output
* 1) got null pointer
* 2) got illegal array store
* 3) got illegal class cast
*/
public class TestExceptions {
public static void main (String [ ] args) {
________________ ;
try {
________________ ;
} catch (NullPointerException e) {
System.out.println ("got null pointer");
}
try {
________________ ;
} catch (ArrayStoreException e) {
System.out.println ("got illegal array store");
}
try {
________________ ;
} catch (ClassCastException e) {
System.out.println ("got illegal class cast");
}
}
}Hint: If you're not sure what kinds of errors these exceptions are for, you can look them up in the Java documentation. If you don't happen to remember the link, googling the name of the exception will likely turn it up.
Throwing Exceptions
If your code may produce a checked exception, you have two choices. One is to
catch the exception. The other is to "pass the buck" by saying
throws exceptionName in the method header. This puts responsibility on the
calling method either to handle the exception or pass the exception to its
caller.
To throw an exception, we use the throw operator and give it a newly
created exception as argument. For example, if a scanned value must be
positive, we could have the following:
k = intScan.nextInt();
if (k <= 0) {
throw new IllegalArgumentException("value must be positive");
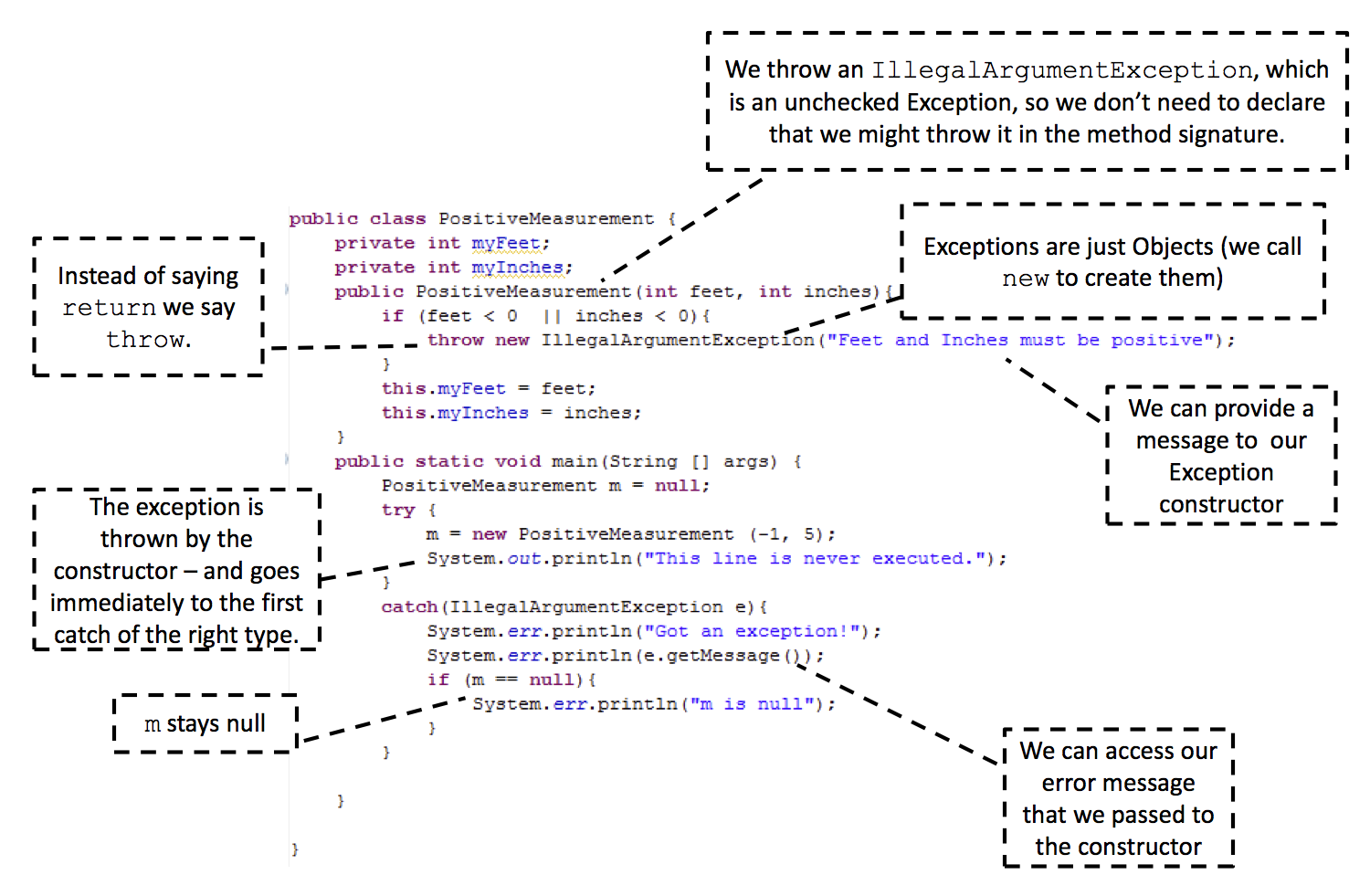
}The programmer can easily define his or her own exceptions by extending
Exception or RuntimeException. Each has two constructors to override,
one with no arguments, the other with a String argument in which an error
message is stored. Here's an example.
class Disaster extends RuntimeException {
public Disaster() {
super();
}
public Disaster(String msg) {
super(msg);
}
}In the exception-catching code, we may access the String argument to the
Exception constructor via the getMessage() method.
Example: Time Input
The code at the bottom of the page is also in Time.java.
It represents a time of day in military time, storing a number of hours
that's between 0 and 23 and a number of minutes between 0 and 59.
Here is a method for testing the constructor, suitable for pasting into a JUnit file.
public void testConstructor() {
String[] timeArgs = {null, "x", "x:", ":x", "x:y", "1:", ":30",
"4: 35", "55:00", "11:99", " 3:30", "00004:45", "4:007", "4:7",
"4 :09", "3:30", "11:55"};
Time[] correctTimes = {null, null, null, null, null, null, null,
null, null, null, null, null, null, null, null,
new Time (3, 30), new Time (11, 55)};
for (int k = 0; k < timeArgs.length; k++) {
Time t = new Time(timeArgs[k]);
assertEquals(correctTimes[k], t);
}
}Now do the following:
Modify the
testConstructormethod:- Surround the call to the
Timeconstructor withtry catch. In the catch block, print the corresponding error message, and make sure that the correspondingcorrectTimesentry isnull, that is, the constructor call threw an exception as it was supposed to. - If the constructor call didn't throw an exception, compare the
constructed result with the corresponding
correctTimesentry as in the existing code.
- Surround the call to the
- Within the
Timeconstructor, catch all exceptions that arise and handle them by throwing anIllegalArgumentExceptionwith an informative message string.
Our solution produces eight different error messages for the given test cases. Cases for illegal times must be tested separately:
- too many leading zeroes in the hours or minutes (e.g. "00007")
- values for hours and minutes that are out of range.
You should add the tests for these cases and throw IllegalArgumentException
with informative message strings.
public class Time {
private int myHours;
private int myMinutes;
public Time(String s) {
int colonPos = s.indexOf(":");
myHours = Integer.parseInt(s.substring(0, colonPos));
myMinutes = Integer.parseInt(s.substring(colonPos+1));
}
public Time(int hours, int minutes) {
myHours = hours;
myMinutes = minutes;
}
public boolean equals(Object obj) {
Time t = (Time) obj;
return myHours == t.myHours && myMinutes == t.myMinutes;
}
public String toString() {
return myHours + ":" + myMinutes;
}
}C. Consistency Checkers
Setting Up Projects
The rest of the lab will involve four main Java files: Date.java, NumberGuesser.java, XsBeforeOs.java and InsertionSort.java. They are located in the lab07 folder.
If you haven't yet switch which partner is coding in this lab, do so now.
Test Driven Development
Each of the tests will check many different cases, especially edge cases. They are all already written for you. This style of workflow, where tests are written before the central code, is called test driven development (it has been mentioned in earlier labs). For the purposes of this lab, do not look at the test files before attempting to complete the method.
Viewing the test cases before writing your code may affect your thinking and cause you to miss thinking about edges cases that might not be tested in the tests. The tests are provided as a black box, intended to check your work while not influencing your code.
If you need help, ask your partner, fellow students, or the staff for help. View the tests only after you have debugged and completed your own work. Viewing the tests after the fact can give you insight into how JUnit 4 tests are constructed. In particular, these tests will show you have you can test that methods will throw exceptions.
Detecting Program Errors
In previous labs, we focused on designing test cases to check results for our code. This is not always the best and most thorough way to look out for bugs, however. Even for simple classes, it is difficult to design a thorough test suite. Secondly, not all aspects of a class (e.g. private instance variables and methods) are accessible to a separate testing class.
In this section, we will introduce the concept of using self-monitoring methods to alert when bugs appear. We will tie the concept of invariants with exception throwing, catching, and handling to check an object's internal state for inconsistencies.
Example: Inconsistencies in Tic-Tac-Toe Boards
Consider a class that represents a board used to play the game of Tic-Tac-Toe, which is played on a three-by-three grid by two players, X and O. Players take turns putting their mark on an empty square of the grid, with X going first. The winner is the player that first puts marks in three horizontal cells, three vertical cells, or three diagonal cells in a row.
Not all possible arrangements of X's and O's in a 3x3 grid will occur in a legal Tic-Tac-Toe game. For example, a board containing nine X's will never appear. Inconsistencies in a Tic-Tac-Toe playing program would thus be represented by impossible boards. The consistency checker would check for these impossible boards, and signal an error if any of them arise.
Discussion: Internally Consistent Boards
Link to the discussionWhat kinds of Tic-Tac-Toe boards are legal?
Consistency Checker for Tic-Tac-Toe Boards
In a Tic-Tac-Toe playing program, we might see the following pseudocode:
Process an X move.
Check the board for consistency.
Repeat the following:
Process an O move.
Check the board for consistency.
If O just won, exit the loop.
Process an X move.
Check the board for consistency.
If X just won, exit the loop.The consistency checker is called immediately after executing an operation that changes the board. We won't be implementing a consistency checker for Tic-Tac-Toe, but we will be for other problems in this lab.
In subsequent discussion, we will use the name isOK to refer to the
consistency checking method. We can combine this concept of consistency
checking with what we learned previously in this lab about exceptions.
If the state of the object being checked is internally consistent, the void
isOK method should not do anything. However, if the object being checked
is not internally consistent, isOK should throw an exception that can
be handled by the method that called it or by our tests. Usually, when you
throw an exception, you should also print an informative error message that
can be used with debugging.
Example: Consistency Checker for Dates
Consider the representation of a date (year, month, day) as three integers:
- year: value between 1900 and 2100
- month: value between 1 and 12 (inclusive), with 1 representing January, 2 representing February, etc
- day: value between 1 and 28, between 1 and 29, between 1 and 30, or between 1 and 31, depending on the month and year
The three integers are the instance variables of a Date class that we are
providing you. The methods include a constructor and an incomplete isOK.
Open the Date.java file and fill out the isOK method that throws an
IllegalStateException (which is built into Java) if the instance variable's
values do not represent a legal date in a year between 1900 and 2100, inclusive.
Test your work by compiling and running the DateTest.java file. It should
pass all the tests.
Example: Efficient (Though Buggy) Number Guessing
The NumberGuesser class uses the binary search technique to guess the
user's number. Binary search starts with a range of values in sorted order—
here, the integers between 0 and 20 (inclusive). To find a particular value, we
first look at the middle value in the range. If the middle value is not what
we're looking for, we check whether what we want is higher or lower than the
middle value. If it's higher, we don't need to search the lower values; if
it's lower, we don't need to search the higher values.
This elimination of (roughly) half the candidates from contention with each iteration yields a much faster algorithm than searching all the candidates one by one with a linear search.
Here's a sample dialog with the program.
Please think of an integer between 0 and 20 (inclusive).
Is your number 10? (Type y or n.) n
Is 10 too high? (Type y or n.) y
Is your number 5? (Type y or n.) n
Is 5 too high? (Type y or n.) n
Is your number 7? (Type y or n.) n
Is 7 too high? (Type y or n.) n
Is your number 8? (Type y or n.) y
Got it!The code uses variables low and high to keep track of the range of values
that are currently candidates for the secret number. low starts out at 0 and
high at 20, reflecting the assumption that the user's number is somewhere
between 0 and 20 (inclusive). At each guess, the program shrinks the range of
values that can contain the user's value, either by lowering high (and
discarding large values) or by raising low (discarding small values).
The program includes a consistency checker isOK method that makes sure that
0 <= low <= high <= 20, and each unsuccessful guess removes the guess from
consideration for the duration of the game.
The program has a bug, however. The number-guessing code and the isOK
method are inconsistent. You'll identify the bug in the next step.
On a side note, notice that this particular isOK method is not void but
rather returns a boolean. This is also a possibility you could use when
working with your own consistency checkers.
#### Self-test: Identifying the Inconsistency
Some of the statements in the NumberGuesser program are numbered (1, 2, etc.). One or more of the numbered statements is buggy. Luckily, isOk will catch the error, and alert you when something goes wrong. Identify which statement is the problem.
|
|
Incorrect
|
|
2 |
Incorrect
|
|
3 |
Incorrect
|
|
4 |
Incorrect
|
|
5 |
Correct
|
|
6 |
Incorrect
|
|
7 |
Incorrect
|
Discussion: Fixing the Bug
Link to the discussion
First fix the statements you just identified. Now the
isOk
check should never fail (assuming the user does not lie to the program). Then briefly explain what you fixed and why it solves the problem.
D. Invariant Relationships
Invariant Relations
A more formal term for the relationships between variables that our isOK
methods are verifying is invariants. "Invariant" means "not varying" or
"not changing". There are two kinds of invariant relationships:
- Class invariants relate values of instance variables to one another. These invariants are also known as representation invariants or data invariants. The "not varying" property is set up initially in the class constructors, and should also hold between calls to the other methods. Inside a method call, the invariant relationship may get temporarily invalidated, but it's restored by the time the method exits.
- Loop invariants relate values of variables in a loop or recursion. The "not varying" property is set up the first time at the start of a loop or at the initial call to a recursive method, and should hold at the end of each loop iteration. Within the loop, the invariant relationship may get temporarily invalidated, but it's restored by the end of the iteration.
The Tic-Tac-Toe board consistency checker contains a class invariant. The board class invariant relates the number of X's and O's in the board. After each move, the number of X's or O's will change, but the relationship between them will still hold (not more O's than X's, and no more than one X more than the number of O's).
The date example also contained a class invariant because the date invariant
relates the year, month, and date-in-month. Updating a date object with
something like a setToTomorrow method (code below) may temporarily invalidate
the relationship, but the relationship will be restored prior to exiting
the method.
public void setToTomorrow ( ) {
myDateInMonth++;
// This may invalidate the invariant relationship
// if tomorrow is the first day of the next month.
if (myDateInMonth > monthLength (myMonth)) {
myMonth++;
if (myMonth == 13) {
myMonth = 1;
}
myDateInMonth = 1; // restore the invariant relationship
}
}The buggy number guesser contains an example of a loop invariant. The invariant related the value-to-be-guessed to the range of values that could contain it, and to the sequence of previous guesses. (The bug in the code resulted from incorrectly maintaining that relationship.)
Loop Invariants with Array Processing
Here is a common invariant pattern that shows up in array processing. The
processing involves a loop. In this case, the array is called values:
for (int k = 0; k < values.length; k++) {
Process element k of values.
}Often the processing of element k consists of including it somehow among elements 0, 1, ..., k–1. The loop invariant property says something about the first k elements or elements 0, 1, ..., k. Thus the invariant pattern is:
for (int k = 0; k < values.length; k++) {
// At this point, the invariant is valid for the subarray
// that contains elements 0, 1, ..., k–1 of values.
Process element k of values.
// At this point, the invariant is valid for the subarray
// that contains elements 0, 1, ..., k of values.
}Loop Invariant Example: Moving X's to Precede O's
Suppose we have a character array that contains X's and O's, and we want to rearrange the contents of this array so that all the X's precede all the O's, as shown in the example below:
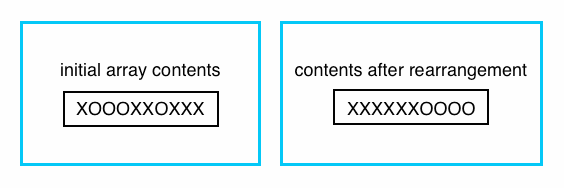
One way to do this is to loop through the array with an index variable named
k, maintaining the invariant that all the X's in the first k elements precede
all the O's. We must also keep track of the position of the last X among
those elements; we'll call that lastXpos. Each loop iteration will start by
examining element k. If it's an O, the invariant is easy to extend, as shown
below.
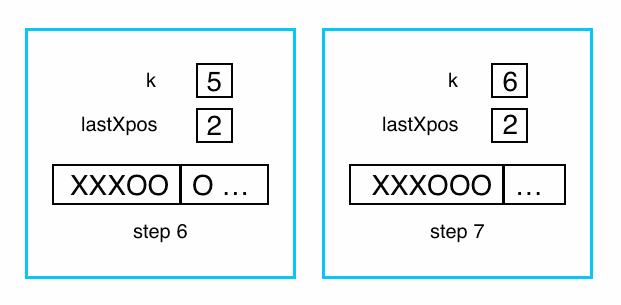
The more complicated case is when element k is an X. To restore the
invariant, we exchange element k with the position of the first O, as in
the following diagram.
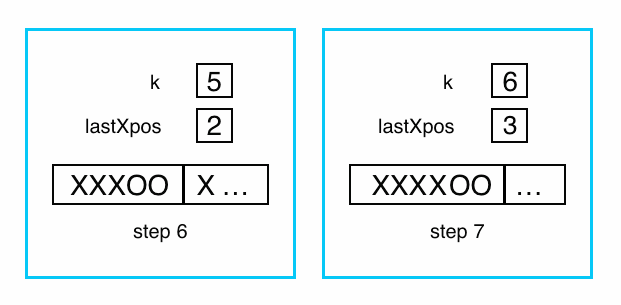
Incidentally, a similar algorithm is used in the Quicksort sorting method that will be covered later in this course.
In the XsBeforeOs class, fill out the isOK method. Given a char array
values and an index variable k, isOK should check that in the first k
elements of values all the Xs precede all the Os. If this consistency
check is not satisfied, isOK should throw an IllegalStateException,
which is built into Java.
After you have completed this method. Compile and run using the instructions provided earlier in the lab. Your code should pass two tests.
Now complete the rearrange method based on the framework given in the
XsBeforeOs class. After completing this method, remove the two @Ignore
annotations before the two rearrange tests in XsBeforeOsTest.java. Compile
and run again. This time, your code should pass all four tests and should not
be printing any error messages.
Exercise: Insertion Sort
Here's another application of the same pattern to sorting the elements of an array. The algorithm is called insertion sort. We will revisit it later. Pseudocode appears below.
for (int k = 1; k < values.length; k++) {
// Elements 0 through k-1 are in nondecreasing order:
// values[0] <= values[1] <= ... <= values[k-1].
// Insert element k into its correct position, so that
// values[0] <= values[1] <= ... <= values[k].
...
}Here's how insertion sort is supposed to work. At the start of the kth time
through the loop, the leftmost k elements of the values array are in order.
The loop body inserts values[k] into its proper place among the first k
elements (probably moving some of those elements up one position in the array),
resulting in the first k+1 elements of the array being in order. The table
below shows a sample array being sorted.
| k | array at start of loop body | array at end of loop body | comments |
|---|---|---|---|
| 1 | 3, 1, 5, 4, 2 | 1, 3, 5, 4, 2 | first two elements in order |
| 2 | 1, 3, 5, 4, 2 | 1, 3, 5, 4, 2 | first three elements in order |
| 3 | 1, 3, 5, 4, 2 | 1, 3, 4, 5, 2 | first four elements in order |
| 4 | 1, 3, 4, 5, 2 | 1, 2, 3, 4, 5 | whole array in order |
Open InsertionSort.java. While this class compiles as we've presented it to
you, it doesn't yet work correctly. The bodies of the methods insert and
isOK are both missing.
Before filling out the isOK and insert methods, open InsertionSortTest.java
and create three additional tests. Examples are given for you. After you have
finished writing your tests, continue to fill out the isOK and insert
methods.
Given an array of ints named list and an index k into the array, isOK
should throw an IllegalStateException when elements 0 through k of list
are not sorted in increasing order. It does nothing if they are sorted
correctly. In the case where k is negative or k exceeds the maximum list
index, isOK should also throw an exception.
Also fill in the body for the insert method, which takes the kth element
of a array and inserts it correctly into the array so that the first k + 1
elements are sorted correctly.
After you have filled out both methods, compile and run the tests. You should pass all six tests, three of which were provided by us and three of which were written by you and your partner.
E. Conclusion
Summary
The lab activities for today included two applications of exceptions. One is checking user input in multiple fields for correctness. Our solution involves cascading tests, first for null input, then empty input, then incorrectly formatted input (too few or too many fields), then incorrect values within a field.
The other is checking internal state of an object for consistency. We saw several examples of "isOK" methods, which check that internal information for the objects is logically consistent. Some of these checks involve class invariant relations (e.g. in the TicTacToe and Date classes), while others involve loop invariant relations (the number-guessing code, the "moving X's to precede O's" code, and insertion sort). We observed a pattern for loop invariants among array values:
for (int k=0; k<values.length; k++){
// At this point, the invariant is valid for the subarray
// that contains elements 0, 1, ..., k-1 of values.
Process element k of values.
// At this point, the invariant is valid for the subarray
// that contains elements 0, 1, ..., k of values.
}Readings
Read the following:
- HFJ chapter 10, pages 539-545, 548, and 568-575Submission
Files to submit for this lab:
- TestExceptions.java
- Time.java
- Date.java
- NumberGuesser.java
- XsBeforeOs.java
- InsertionSort.java
- InsertionSortTest.java
Submit these files as lab07.
In addition, please fill out this self-reflection form before this lab is due, as a part of your lab assignment. Self-reflection forms are to be completed individually, not in partnership.