We have provided the skeleton file lab8.py for you to write your solutions in (it includes rlist functions for you to use). You can also copy it to your account by using the following in your terminal:
cp ~cs61a/lib/lab/lab8.py .
For the following 2 questions, write both an iterative solution (uses a while or for loop) and a recursive solution (no while or for loops).
0.) Write a function contains that takes a number n as the first argument and a rlist of numbers l as the second argument, and returns whether n is in l.
1.) The greatest common divisor of two positive integers a and b is the largest integer which evenly divides both numbers (with no remainder). Euclid, a Greek mathematician in 300 BC, realized that the greatest common divisor of a and b is the smaller value if it evenly divides the larger value or the same as the greatest common divisor of the smaller value and the remainder of the larger value divided by the smaller value. So if a is greater than b and a is not divisible by b then:
gcd(a, b) == gcd(b, a % b)
Write the gcd function using Euclid's algorithm.
2.) It is a common problem to find whether an element p exists in a sorted list. There is an efficient algorithm known as binary search that cuts the number of elements you are currently looking through by 50% at each iteration. Each iteration of binary_search works like this.
Write a recursive solution for binary_search. Given an element and a list, it should return True if the element in the list, and False otherwise. When there is no clear "middle" element of the list (ie. when the list is even) take the smaller of the two middle elements. Also, never include the middle element when slicing the list for the next iteration (otherwise the function might never stop).
3.) Write the function deep_map, which works almost the same as map except that if one of the items is a list, we also apply the function to each of its items. Here are some examples of how deep_map should work:
>>> deep_map(lambda x: x * x, [1, 2, [3, [4], 5], 6]) [1, 4, [9, [16], 25], 36] >>> deep_map(lambda x: x + 2, [4, 22, [23, 35], 9]) [6, 24, [25, 37], 11]
4.) Consider an insect in a MxN grid. The insect starts at the top left corner, (0,0), and wants to end up at the bottom right corner, (M-1,N-1). The insect is only capable of moving right or down. Write a function count_paths that takes a grid length and width and returns the number of different paths the insect can take from the start to the goal. [There is an analytic solution to this problem, but try to answer it procedurally using recursion].
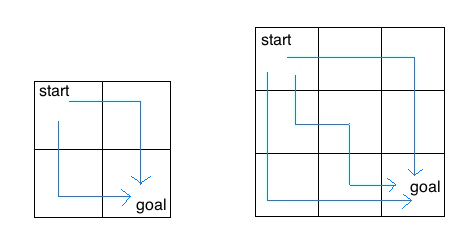
For example, the 2x2 grid has a total of two ways for the insect to move from the start to the goal. For the 3x3 grid, the insect has 6 different paths (only 3 are shown above).