We've provided a starter file with skeleton code for the exercises in the lab. You can get it at the following link:
You can find additional practice problems from this lab on OOP from Spring 2013 helpful.
Problem 1: Consider the following code:
class Animal(object):
def __init__(self):
self.is_alive = True # It's alive!!
class Pet(Animal):
def __init__(self, name, year_of_birth, owner=None):
Animal.__init__(self) # call the parent's constructor
self.name = name
self.age = current_year - year_of_birth
self.owner = owner
def eat(self, thing):
print(self.name + " ate a " + str(thing) + "!")
def talk(self):
print("...")
Implement a Cat class that inherits from Pet. Use superclass
methods wherever possible.
class Cat(Pet):
def __init__(self, name, year_of_birth, owner, lives=9):
"*** YOUR CODE HERE ***"
def talk(self):
"""A cat says 'Meow!' when asked to talk."""
"*** YOUR CODE HERE ***"
def lose_life(self):
"""A cat can only lose a life if they have at least one
life. When there are zero lives left, the 'is_alive'
variable becomes False.
"""
"*** YOUR CODE HERE ***"
Problem 2: Now implement a NoisyCat class, which inherits from
Cat. A NoisyCat is just like a normal Cat except, when asked to
talk, it says what a normal Cat says twice.
class NoisyCat(Cat):
def __init__(self, name, year_of_birth, owner, lives=9):
"*** YOUR CODE HERE ***"
# hint: do you need to write another __init__?
def talk(self):
"""A NoisyCat will always repeat what he/she said
twice."""
"*** YOUR CODE HERE ***"
In lecture, we introduced the OOP version of an Rlist:
class Rlist:
"""A recursive list consisting of a first element and the rest.
>>> s = Rlist(1, Rlist(2, Rlist(3)))
>>> print(rlist_expression(s.rest))
Rlist(2, Rlist(3))
>>> len(s)
3
>>> s[1]
2
"""
class EmptyList:
def __len__(self):
return 0
empty = EmptyList()
def __init__(self, first, rest=empty):
self.first = first
self.rest = rest
def __getitem__(self, i):
if i == 0:
return self.first
else:
return self.rest[i-1]
def __len__(self):
return 1 + len(self.rest)
Just like before, these Rlists have a first and a rest. The difference is
that, now, the Rlists are mutable.
To check if an Rlist is empty, compare it against the class variable
Rlist.empty:
if rlist is Rlist.empty:
return 'This rlist is empty!'
Don't construct another EmptyList!
In this lab, we will be using rlist_expression to print a string
representation of an Rlist.
def rlist_expression(s):
"""Return a string that would evaluate to s."""
if s.rest is Rlist.empty:
rest = ''
else:
rest = ', ' + rlist_expression(s.rest)
return 'Rlist({0}{1})'.format(s.first, rest)
Problem 3: Predict what Python will display when the following lines are typed into the interpreter:
>>> print(rlist_expression(Rlist(1, Rlist(2))))
_____
>>> Rlist()
_____
>>> rlist = Rlist(1, Rlist(2, Rlist(3)))
>>> rlist.first
_____
>>> rlist.rest.first
_____
>>> rlist.rest.rest.rest is Rlist.empty
_____
>>> rlist.first = 9001
>>> rlist.first
_____
>>> rlist.rest = rlist.rest.rest
>>> rlist.rest.first
_____
>>> rlist = Rlist(1)
>>> rlist.rest = rlist
>>> rlist.rest.rest.rest.rest.first
_____
A recursive list can be represented as a series of Rlist constructors, where
Rlist.rest is either another recursive list or the empty list.
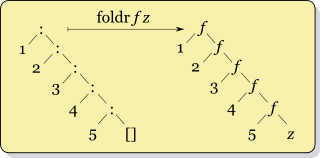
We represent such a list in the diagram below:

In this diagram, the recursive list
Rlist(1, Rlist(2, Rlist(3, Rlist(4,Rlist(5)))))
is represented with : as the constructor and [] as the empty list.
We define a function foldr that takes in a function f which takes two
arguments, and a value z. foldr essentially replaces the Rlist constructor
with f, and the empty list with z. It then evaluates the expression and
returns the result. This is equivalent to:
f(1, f(2, f(3, f(4, f(5, z)))))
We call this operation a right fold.
Similarily we can define a left fold foldl that folds a list starting from the
beginning, such that the function f will be applied this way:
f(f(f(f(f(z, 1), 2), 3), 4), 5)
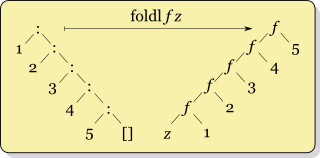
Also notice that a left fold is equivilant to python's reduce with 3 arguments.
Problem 4: Write the left fold function by filling in the blanks.
def foldl(rlist, fn, z):
""" Left fold
>>> lst = Rlist(3, Rlist(2, Rlist(1)))
>>> foldl(lst, sub, 0) # (((0 - 3) - 2) - 1)
-6
>>> foldl(lst, add, 0) # (((0 + 3) + 2) + 1)
6
>>> foldl(lst, mul, 1) # (((1 * 3) * 2) * 1)
6
"""
if rlist is Rlist.empty:
return z
return foldl(______, ______, ______)
Problem 5: Now write the right fold function.
def foldr(rlist, fn, z):
""" Right fold
>>> lst = Rlist(3, Rlist(2, Rlist(1)))
>>> foldr(lst, sub, 0) # (3 - (2 - (1 - 0)))
2
>>> foldr(lst, add, 0) # (3 + (2 + (1 + 0)))
6
>>> foldr(lst, mul, 1) # (3 * (2 * (1 * 1)))
6
"""
"*** YOUR CODE HERE ***"
Now that we've written the fold functions, let's write some useful functions using list folding!
Problem 6: Write the mapl function, which takes in a Rlist lst and a
function fn, and returns a new Rlist where every element is the function
applied to every element of the original list. Use either foldl or
foldr. Hint: it is much easier to write with one of them than the other!
def mapl(lst, fn):
""" Maps FN on LST
>>> lst = Rlist(3, Rlist(2, Rlist(1)))
>>> mapped = mapl(lst, lambda x: x*x)
>>> print(rlist_expression(mapped))
Rlist(9, Rlist(4, Rlist(1)))
"""
"*** YOUR CODE HERE ***"
Problem 7: Write the filterl function, using either foldl or foldr.
def filterl(lst, pred):
""" Filters LST based on PRED
>>> list = Rlist(4, Rlist(3, Rlist(2, Rlist(1))))
>>> filtered = filterl(lst, lambda x: x % 2 == 0)
>>> print(rlist_expression(filtered))
Rlist(4, Rlist(2))
"""
"*** YOUR CODE HERE ***"
Problem 8: Use foldl to write reverse, which takes in a recursive list and
reverses it. Hint: It only takes one line!
def reverse(lst):
""" Reverses LST with foldl
>>> reversed = reverse(Rlist(3, Rlist(2, Rlist(1))))
>>> print(rlist_expression(reversed))
Rlist(1, Rlist(2, Rlist(3)))
>>> reversed = reverse(Rlist(1))
>>> print(rlist_expression(reversed))
Rlist(1)
>>> reversed = reverse(Rlist.empty)
>>> reversed == Rlist.empty
True
"""
"*** YOUR CODE HERE ***"
Extra for experts: Write a version of reverse that do not use the Rlist
constructor. You do not have to use foldl or foldr.
Problem 9 Extra for Experts: Write foldl using foldr! You only need to fill
in the step function.
def foldl2(rlist, fn, z):
""" Write foldl using foldr
>>> list = Rlist(3, Rlist(2, Rlist(1)))
>>> foldl2(list, sub, 0) # (((0 - 3) - 2) - 1)
-6
>>> foldl2(list, add, 0) # (((0 + 3) + 2) + 1)
6
>>> foldl2(list, mul, 1) # (((1 * 3) * 2) * 1)
6
"""
def step(x, g):
"*** YOUR CODE HERE ***"
return foldr(rlist, step, identity)(z)
Trees are a way we have of representing a hierarchy of information. A family tree is a good example of something with a tree structure. You have a matriarch and a patriarch followed by all the descendants. Alternately, we may want to organize a series of information geographically. At the very top, we have the world, but below that we have countries, then states, then cities. We can also decompose arithmetic operations into something much the same way.
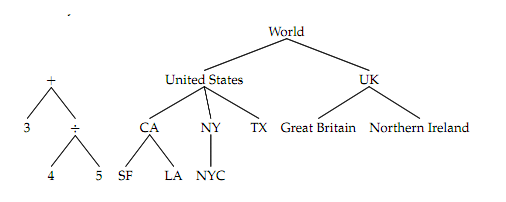
The name "tree" comes from the branching structure of the pictures, like real trees in nature except that they're drawn with the root at the top and the leaves at the bottom.
Terminology
In this course, we will only be working with binary trees, where each node as at most two children. For a general binary tree, order does not matter. Additionally, the tree does not have to be balanced. It can be as lopsided as one long chain.
Our implementation of binary trees can be found in lab6.py:
class Tree:
def __init__(self, entry, left=None, right=None):
self.entry = entry
self.left = left
self.right = right
def copy(self):
left = self.left.copy() if self.left else None
right = self.right.copy() if self.right else None
return Tree(self.entry, left, right)
We also included a function tree_string, which prints out a string
representation of a tree:
>>> print(tree_string(Tree(1, Tree(3, None, Tree(2)), Tree(4, Tree(5), Tree(6)))))
-1-
/ \
3 4
\ / \
2 5 6
Problem 10: Define the function size_of_tree which takes in a tree as an
argument and returns the number of non-empty nodes in the tree.
def size_of_tree(tree):
r""" Return the number of non-empty nodes in TREE
>>> print(tree_string(t)) # doctest: +NORMALIZE_WHITESPACE
-4--
/ \
2 1-
/ \ / \
8 3 5 3
/ / \ / \
7 1 6 2 9
>>> size_of_tree(t)
12
"""
"*** YOUR CODE HERE ***"
Problem 11: Define the function deep_tree_reverse, which takes a tree and
reverses the given order.
def deep_tree_reverse(tree):
r""" Reverses the order of a tree
>>> a = t.copy()
>>> deep_tree_reverse(a)
>>> print(tree_string(a)) # doctest: +NORMALIZE_WHITESPACE
--4---
/ \
1- 2-
/ \ / \
3 5 3 8
/ \ / \ \
9 2 6 1 7
"""
"*** YOUR CODE HERE ***"
Problem 12: Define the function filter_tree which takes in a tree as an
argument and returns the same tree, but with items included or excluded based
on the pred argument.
Note that there is ambiguity about what excluding a tree means. For this function, when you exclude a subtree, you exclude all of its children as well.
def filter_tree(tree, pred):
r""" Removes TREE if entry of TREE satisfies PRED
>>> a = t.copy()
>>> filtered = filter_tree(a, lambda x: x % 2 == 0)
>>> print(tree_string(filtered)) # doctest: +NORMALIZE_WHITESPACE
4
/
2
/
8
>>> a = t.copy()
>>> filtered = filter_tree(a, lambda x : x > 2)
>>> print(tree_string(filtered))
4
"""
"*** YOUR CODE HERE ***"
Problem 13: Define the function max_of_tree which takes in a tree as an
argument and returns the max of all of the values of each node in the tree.
def max_of_tree(tree):
r""" Returns the max of all the values of each node in TREE
>>> print(tree_string(t)) # doctest: +NORMALIZE_WHITESPACE
-4--
/ \
2 1-
/ \ / \
8 3 5 3
/ / \ / \
7 1 6 2 9
>>> max_of_tree(t)
9
"""
"*** YOUR CODE HERE ***"