Homework 10
Due: Monday, 11/14 @ 5pm
To complete this homework, you will need access to a Logo interpreter. We recommend UCBLogo, of course. It is installed on instructional machines as logo and available as a free download for Mac, Unix, and Windows.
If you have difficulty using an installed version of Logo, you may find this browser-based Logo implementation useful for development. Warning: it may not behave identically to UCB Logo.
The staff solutions to these problems do not use the make (assignment) procedure at all. For a challenge, try not to use make yourself.
The Logo starter file, hw10.lg contains procedure stubs and tests.
Background: Huffman Encoding Trees
We consider the problem of representing text as a sequence of ones and zeros (bits). For example, the ASCII standard code used to represent text in computers encodes each character as a sequence of seven bits, and 128 characters are encoded in total. In general, if we want to distinguish n different symbols, we will need to use log base 2 of n bits per symbol.
As a simpler example, consider encoding only A, B, C, D, E, F, G, and H. We can choose a code with three bits per character, for example:
A 000 C 010 E 100 G 110 B 001 D 011 F 101 H 111
With this code, the message:
BACADAEAFABBAAAGAH
is encoded as the string of 54 bits:
001000010000011000100000101000001001000000000110000111
Codes such as ASCII and the A-through-H code above are known as fixed-length codes, because they represent each symbol in the message with the same number of bits. It is sometimes advantageous to use variable-length codes, in which different symbols may be represented by different numbers of bits. If our messages are such that some symbols appear very frequently and some very rarely, we can encode data more efficiently (i.e., using fewer bits per message) if we assign shorter codes to the frequent symbols. Consider the following alternative code for the letters A through H:
A 0 C 1010 E 1100 G 1110 B 100 D 1011 F 1101 H 1111
With this code, the same message as above is encoded as the string:
100010100101101100011010100100000111001111
This string contains 42 bits, so it saves more than 20% in space in comparison with the fixed-length code shown above.
One of the difficulties of using a variable-length code is knowing when you have reached the end of a symbol in reading a sequence of zeros and ones. One solution is to design the code in such a way that no complete code for any symbol is the beginning (or prefix) of the code for another symbol. Such a code is called a prefix code. In the example above, A is encoded by 0 and B is encoded by 100, so no other symbol can have a code that begins with 0 or with 100.
In general, we can attain significant savings if we use variable-length prefix codes that take advantage of the relative frequencies of the symbols in the messages to be encoded. One particular scheme for doing this is called the Huffman encoding method, after its discoverer, David Huffman. A Huffman code can be represented as a binary tree whose leaves are the symbols that are encoded.
Each symbol at a leaf is assigned a weight (which is its relative frequency), and each non-leaf node contains a weight that is the sum of all the weights of the leaves lying below it. The weights are not used in the encoding or the decoding process. We will see below how they are used to help construct the tree.
The figure below shows the Huffman encoding tree for the A-through-H prefix code given above. The weights at the leaves indicate that the tree was designed for messages in which A appears with relative frequency 8, B with relative frequency 3, and the other letters each with relative frequency 1.
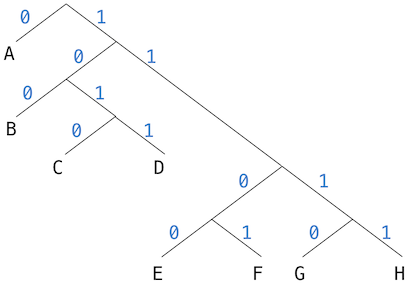
Decoding
To decode a bit sequence using a Huffman tree, we begin at the root and use the successive zeros and ones of the bit sequence to determine whether to move down the left or the right branch. Each time we come to a leaf, we have generated a new symbol in the message, at which point we start over from the root of the tree to find the next symbol.
For example, suppose we are given the tree above and the sequence:
10001010
Starting at the root, we move down the right branch, (since the first bit of the string is 1), then down the left branch (since the second bit is 0), then down the left branch (since the third bit is also 0). This brings us to the leaf for B, so the first symbol of the decoded message is B.
Now we start again at the root, and we make a left move because the next bit in the string is 0. This brings us to the leaf for A. Then we start again at the root with the rest of the string 1010, so we move right, left, right, left and reach C. Thus, the entire message is BAC.
Encoding
Given a Huffman tree, we can enumerate the codes of all letters by traversing the tree. That is, we can write a function that takes as input the tree and returns a list of letter-code pairs that gives the code for each letter. Then, encoding a message involves concatenating the code for each letter in the message.
Generating Huffman Encoding Trees
Given an alphabet of symbols and their relative frequencies, how do we construct the tree that will encode messages with the fewest bits? Huffman gave an algorithm for doing this and showed that the resulting code is indeed the best variable-length code for messages where the relative frequency of the symbols matches the frequencies with which the code was constructed.
The algorithm for generating a Huffman tree is very simple. The idea is to arrange the tree so that the symbols with the lowest frequency appear farthest away from the root. Begin with the set of leaf nodes, containing symbols and their frequencies, as determined by the initial data from which the code is to be constructed. Now find two leaves with the lowest weights and merge them to produce a node that has these two nodes as its left and right branches. The weight of the new node is the sum of the two weights. Remove the two leaves from the original set and replace them by this new node.
Now continue this process. At each step, merge two nodes with the smallest weights, removing them from the set and replacing them with a node that has these two as its left and right branches. The process stops when there is only one node left, which is the root of the entire tree. Here is how the previous example Huffman tree is generated, where trees are described by the set of letter they contain, along with their weight:
Initial leaves:
{(A 8) (B 3) (C 1) (D 1) (E 1) (F 1) (G 1) (H 1)}
{(A 8) (B 3) ({C D} 2) (E 1) (F 1) (G 1) (H 1)}
{(A 8) (B 3) ({C D} 2) ({E F} 2) (G 1) (H 1)}
{(A 8) (B 3) ({C D} 2) ({E F} 2) ({G H} 2)}
{(A 8) (B 3) ({C D} 2) ({E F G H} 4)}
{(A 8) ({B C D} 5) ({E F G H} 4)}
{(A 8) ({B C D E F G H} 9)}
{({A B C D E F G H} 17)}
The algorithm does not always specify a unique tree, because there may not be unique smallest-weight nodes at each step. Also, the choice of the order in which the two nodes are merged (i.e., which will be the right branch and which will be the left branch) is arbitrary.
Question 1: Implementing Huffman Encoding Trees
(1A) Complete this abstract data type for representing a Huffman encoding tree. Leaves of the tree are represented by a sentence consisting of the word "leaf", the letter at the leaf, and the weight.
A Huffman encoding tree consists of a branch0, a branch1, and a weight. When we make a tree, we obtain the weight of the tree as the sum of the weights of the input trees (or leaves). By storing the weight as the third element of a tree, we can reuse the weight procedure for leaves to retrieve the weight of trees as well.
(1B) Implement decode_one, which takes as arguments a Huffman encoding tree and a word that consists of zeros and ones. It outputs the same word, but with the first letter decoded. The word procedure concatenates two words. The first and butfirst procedures can apply to either words or sentences.
(1C) Implement encodings, a procedure that returns a sentence of two-element sentences (pairs). Each of these pairs contains a letter and an encoding for that letter. The input is a Huffman encoding tree, and the output contains all letters encoded in that tree. The output should be ordered according to the order of leaves in a left-to-right traversal of the tree.
Hint: Feel free to introduce a helper procedure.
(1D) Implement Huffman, a procedure that takes a sentence of trees (or leaves) and outputs an optimal Huffman encoding tree. The elements of the input sentence are sorted from lowest to highest weight.
Hint: Keep the input to recursive calls to Huffman sorted, by using the provided insert procedure, which always outputs a sorted sentence.
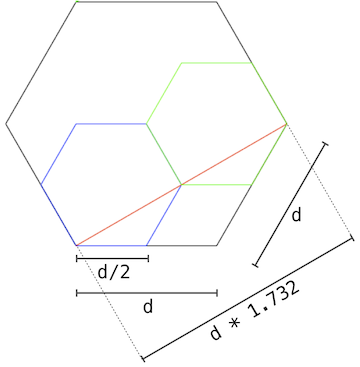
Question 2: Recursive Hexagons
Write a procedure called hax that draws the following recursive illustration when passed two arguments, a side length d and recursive depth k. In this example, k is 5.
To see how this illustration is constructed, consider this annotated version that gives the relative lengths of lines of the component shapes in the figure.