Written Assignment 4: Bayes' Nets
Due 3/23 at 11:59pm
UPDATE: 3/19, Assignment is now complete, point values
have been re-allocated.
UPDATE: 3/22, Slight clarification to problem 4.
Question 1 (4 points). Consider the following basic
Bayes' net, in which X, Y, and Z are Boolean variables:
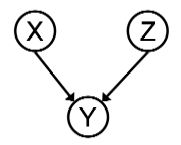
-
Prove that X and Z are (marginally) independent, for any choice of the
local conditional probabilities.
-
Exhibit a set of local conditional probabilities with the property that
X and Z are also conditionally independent given Y. (You may wish to use the
applet referred to in problem 3 to test out your distributions painlessly.)
-
Exhibit a set of local conditional probabilities with the property that,
given Y = true, X and Z exhibit a negative correlation (explaining-away).
That is, P(X = true | Y = true) > P(X = true), but P(X = true | Y = true, Z =
true) < P(X = true | Y = true). Give an intuitive scenario where this
trend would hold.
-
Exhibit a set of local conditional probabilities with the property that,
given Y = true, X and Z exhibit a positive correlation. That is, P(X =
true | Y = true) > P(X = true), and P(X = true | Y = true, Z = true) > P(X =
true | Y = true). Give an intuitive scenario where this trend would hold.
Question 2 (4 points). Given the Bayes' net below,
consider each of the listed pairs of variables. For each pair:
- Specify a
minimal set of variables (possibly none) whose observation makes the pair
conditionally independent
- Specify a minimal set of variables (possibly none) for
which the variables may be dependent
- Show a path which connects the
variables using the Bayes' ball (d-separation) reachability algorithm given the
evidence variables you chose above
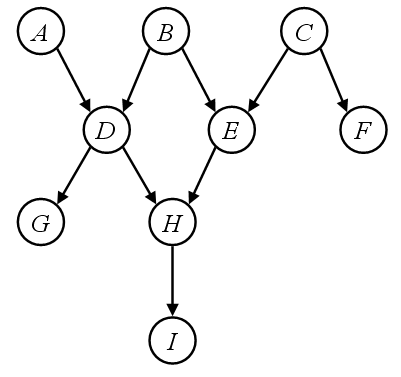
- A and F
- B and I
- G and E
- Which nodes are reachable from A (i.e. not separated, or possibly dependent) given observations
of D and H? What about given C and I?
Question 3 (5 points). Consider the following
domain:
- There are three soccer teams, A, B, and C. Each has a fixed, unknown quality of 0, 1, 2, or 3 (larger is better).
-
Each team plays every other team once, resulting in a win, loss,
or draw.
-
When two teams play,
the result is a noisy, probabilistic function of the difference between their
qualities:
-
If the difference is 0, a team wins 30%, loses 30%, or draws 40% of the time.
-
If the difference is 1, the better team wins 50%, loses 20%, or draws 30%.
-
If the difference is 2, the better team wins 70%, loses 10%, or draws 20%.
-
If the difference is 3, the better team wins 90% or draws 10%.
For the parts which ask for specific calculations, use the Bayes' net applets
at the
UBC CI site or JavaBayes to execute the queries (use the belief network app, not the
decision network one). Parts (c) through (h) should take very little
time with the help of the applet.
- Draw a reasonable Bayes' net for this domain, briefly justifying what
arcs you do and do not include.
- For each node, specify a reasonable local conditional probability table.
If multiple nodes in your network have the same local distributions, you
only need to write those distributions once.
- What is the posterior distribution over the game between B and C, given
no evidence? Does this answer make sense?
- If A beats B, what is the updated posterior distribution over the
outcome of the game between B and C? Does this make sense?
- If A beats B but draws against C, what is the updated posterior distribution over the
outcome of the game between B and C? Does this change make sense?
- If A beats B but draws against C, what are the posterior distributions over the unobserved qualities of each team? Do these distributions make sense?
- If A beats B (and the result of the game against C is unknown), what is
the posterior distribution over C's quality? Why can you answer this question
without any numerical calculations?
- If A is known to have quality 1, what is the posterior distribution over the outcome
of the game between A and B? Does this distribution make sense?
Question 4 (4 points). Consider the following local
conditional probability tables over the domain from lecture, where low pressure
(L)
causes rain (R), which causes both a dripping ceiling (D) and traffic (T).
Traffic in turn causes traffic reports (T') but such reports are often
out-of-date and not all traffic is reported:
| P(L) |
P(R|L) |
P(T|R) |
P(D|R) |
P(T'|T) |
|
|
R |
L |
P |
| r |
l |
0.80 |
| ¬r |
l |
0.20 |
| r |
¬l |
0.10 |
| ¬r |
¬l |
0.90 |
|
T |
R |
P |
| t |
r |
0.70 |
| ¬t |
r |
0.30 |
| t |
¬r |
0.50 |
| ¬t |
¬r |
0.50 |
|
|
D |
R |
P |
| d |
r |
0.50 |
| ¬d |
r |
0.50 |
| d |
¬r |
0.01 |
| ¬d |
¬r |
0.99 |
|
T' |
T |
P |
| t' |
t |
0.75 |
| ¬t' |
t |
0.25 |
| t' |
¬t |
0.25 |
| ¬t' |
¬t |
0.75 |
|
- Draw the Bayes' net corresponding to these tables (i.e. state the the
graph structure given the local tables).
- Assume you are given an initial observation that there is no traffic
report, but there is a low pressure system (note: contradictory evidence).
You wish to calculate the posterior distribution over whether or not it is
raining (R) under these circumstances. What are the initial factors
for this model and observations for the purposes of the variable elimination
algorithm?
- Define and calculate the new factor introduced after eliminating T (show the result after T is both joined and summed out).
- Continuing from the factors after the elimination of T, define and calculate the new factor introduced after eliminating D.
Why does this factor take this special form? In general, for any run
of the variable elimination algorithm, we can completely ignore any variable
which does not have either a query node or an evidence node as a descendent.
- What is the final posterior distribution over R?
Question 5 (3 points). Consider the following Bayes'
net in which a single cause has several indirect effects:
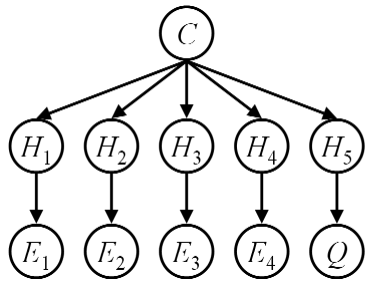
Assume that you wish to predict the posterior distribution over Q given
observations of E1 = e1 through
E4 = e4.
- State the original factors for the variable elimination algorithms in
terms of the local conditional probabilities of the given net.
- Assuming that each variable is Boolean, what is the size of the largest
factor created if all the variables Hi are eliminated first, then C?
- What if C is eliminated first, then all of the Hi are eliminated?
- Argue (very briefly) which order is more efficient and why.



