Written Assignment 2: Constraint Satisfaction Problems
Due 2/14 at 11:59pm
Question 1 (5 points). Consider the following CSP:
Variables: {A, B, C, D}
Domain: {1, 2, 3}
Binary Constraints: A ≠ B, A ≠ C, B > C, B < D
- Draw a constraint graph for this problem and write out the implicit constraints as explicit sets of legal pairs.
- Assuming an alphabetical ordering on both variables and values, show the
assignments considered by each step of backtracking DFS with forward checking.
After each assignment, indicate the remaining domains of all unassigned variables. E.g., completely naive DFS would
search A=1, A=1 B=1, A=1 B=1 C=1, A=1 B=1 C=1 D=1, A=1 B=1 C=1 D=2, A=1 B=1 C=1 D=3, then pop back up to A=1 B=1 C=2, and so on, but never remove any
values from unassigned domains.
- Show the assignments and domains, again with backtracking DFS and forward checking, but now
using the MRV and LCV orderings. (Break MRV ties by the degree
heuristic, then alphabetically; break LCV ties numerically, smaller values first.) Is
this any faster than part (b)? Why or why not?
- Show the assignments and domains, again with backtracking DFS and
forward checking, using the original alphabetical ordering, but now using
cutset conditioning, with C as a cutset. Is there a better cutset?
- Show the assignments and domains with arc consistency
(i.e. AC-3) run as preprocessing at the start and after each assignment.
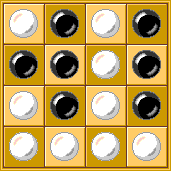
Question 2 (5 points). In the game of Fiver, one
has a grid of black and white squares and repeatedly selects squares to
flip. Each flip changes not only the color of the selected square, but
also the adjacent squares to the north, south, east, and west. Starting
from a given configuration, the goal is to turn all the squares black. For
this problem, assume the all white board is the starting configuration. To
try a game, see this web demo.
 |
|
 |
|
 |
| Start |
|
After selecting (2,3) and (4,3) |
|
Goal |
- Formulate Fiver as a search problem. What are the states (including start and goal),
successor function, and cost function?
- Describe a non-trivial admissible heuristic function for this problem.
- Explain why no optimal solution will select the same square twice.
- Formulate Fiver as a general CSP: what are the variables, domains, and
constraints. Remember that general CSPs may have constraints on any
subset of variables, not only pairs of variables.
- Which formulation do you think will result in a more efficient
solution? Why?
Question 3 (4 points). In this problem, you will
prove that every general CSP (constraints on arbitrary subsets of variables) can
be transformed into an equivalent binary CSP (constraints only on pairs of
variables). You should assume that variables have finite domains.
See p. 159 of the textbook for another wording of this problem (and a hint).
- First, show how unary constraints can be eliminated by altering the
domains of variables.
- Show that any ternary constraint can be transformed into three binary
constraints by introducing a new auxiliary variable.
- Finally, show how a similar approach can be used to transform any n-ary
constraint into a set of binary constraints.
- For n-ary constraints, how many auxiliary variables are introduced? What are their maximum domain sizes? How many binary constraints (arcs in the constraint graph) are required?
Question 4 (6 points). In the game of Minesweeper,
we would like to determine which squares on a grid contain mines. At any
given time, we have a partially revealed board, like the one below:

Squares are either marked as revealed (and therefore clear) or hidden
(possibly a mine, or possibly clear). All revealed squares show the number
of adjacent squares, including diagonals, which have mines (in most programs,
zeros are displayed as blanks). At each step, we select a hidden position
to reveal. We win if we reveal all clear squares without revealing a
mine. We can use CSPs to gather information about unknown squares for a particular state.
You can try a game here.
- Formulate a CSP where a solution is an assignment of the hidden
squares to {clear, mine} which is compatible with the observed adjacent mine
counts. Assume the number of remaining mines is unknown.
- Sometimes we have to guess. Show a small, simple board
configuration for which no hidden square is guaranteed to be clear, and
show the set of solutions to the CSP.
- Sometimes we can reason that a certain hidden position is guaranteed to
be clear. Show a small, simple configuration which has more than one
solution, but where all solutions agree that some currently hidden
position is clear. Show those solutions.
- Why will a standard CSP solver not directly tell us where to move next?
- How can we augment the basic DFS-based backtracking constraint solver to tell us whether or not a square
is guaranteed to be safe.
- Can we still use forward checking with the augmented DFS-based backtracking constraint solver from
part e) ? Why or why not? What about arc consistency?
- [Extra Credit: 1 point] Show a method for correctly deciding which move is safest
when no move is perfectly safe.






