Written Assignment 1: Search
Due 2/2 at 11:59pm
Question 1 (3 points). Write PEAS descriptions for
the following tasks. A correct answer to each task can fit in four lines,
one for each aspect.
- A web-based machine translation system (like Systran)
- A search and rescue robot for exploring a collapsed mine (similar)
- A burrito-building robot
Question 2 (3 points). Consider the following search graph in which A is the start state and F is the goal state. Assume that for each search method, the details are such that a state's children will be visted in alphabetical order when possible.
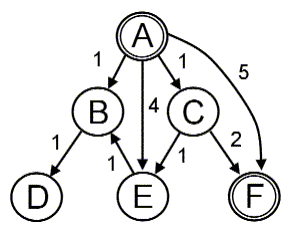
- In what order will the states be expanded by a depth-first tree search (no closed list)?
- In what order will the states be expanded by a breadth-first graph search (with closed list)?
- In what order will the states be expanded by a uniform-cost graph search (with closed list)?
Question 3 (4 points). Burrito assembly scheduling:
You manage a taqueria. Making a burrito requires a set of tasks x1, …, xn. Each task xi
takes ti minutes to complete. Also, some tasks require other tasks to be completed before
they can be begun. You may schedule tasks among your e employees. How fast can you make
a burrito?
Example: You have two (e = 2) employees and the following tasks, with
the following requirements and durations listed:
- Steam tortilla: 1
- Cook steak: 3
- Add beans: 1 (requires steamed tortilla)
- Add cheese: 1 (requires steamed tortilla)
- Add steak: 1 (requires steamed tortilla, cooked steak)
- Wrap burrito: 1 (requires all added)
- Prepare to-go bag: 3
- Collect money from customer: 3
- Put burrito in a prepared bag: 1 (requires wrapped burrito, prepared bag)
A schedule is a set of task/time pairs {(x, t)} such that each task x's prerequisites are completed by time t, and such that
no more than e tasks are being worked on at each time step. The cost of a schedule is the earliest time at which all tasks in that schedule will
be completed. In the end, we are interested in finding minimum cost schedules which accomplish all tasks.
- Why can we think of this scheduling problem a single agent search problem rather than a multi-agent problem?
- Formulate this problem as a single agent search problem. What are the states, successor functions, start state, goal test, and cost function?
- Describe a non-trivial heuristic for this problem.
- How would you modify your formulation if each task could have a different cost for each employee?
Question 4 (5 points). The Traveling Salesperson Problem (TSP) is a frequently studied route planning problem.
In a TSP, one has a set C of cities connected by roads. The length of the direct roads between cities x and y is given by d(x,y); if two cities are
not directly connected by a road, d(x,y) will be infinite. A tour is a list of cities that starts and ends at the same city and visits each
city exactly once. The task is to find a tour of minimum total length. It is impractical to enumerate all tours, so one must devise better, often
approximate, algorithms to solve TSPs.
- Assuming there are N cities and all roads exist, how many distinct tours are there? For this question, assume (a, b, c, a), (b, c, a, b), and (a, c, b, a) are all the same tours.
- Give a formulation which casts the TSP as a single agent search problem in which optimal solutions correspond to TSP solutions. What are the states and successor functions? What is the start state and what
is the goal test? What is the cost of a single action? (Hint: without loss of generality, you may assume that some city s in C is to be the beginning of the tour.)
- If all cities are connected with roads of length 1, compare briefly the behavior of DFS and BFS. Under these circumstances, is DFS complete? Optimal? Is BFS complete? Optimal? Which is better and why?
- If roads have arbitrary length, which of the following will be optimal: DFS, BFS, uniform cost search, greedy search, and/or A* search?
- Give a non-trivial and reasonably efficient admissible heuristic for this problem and prove its admissibility.
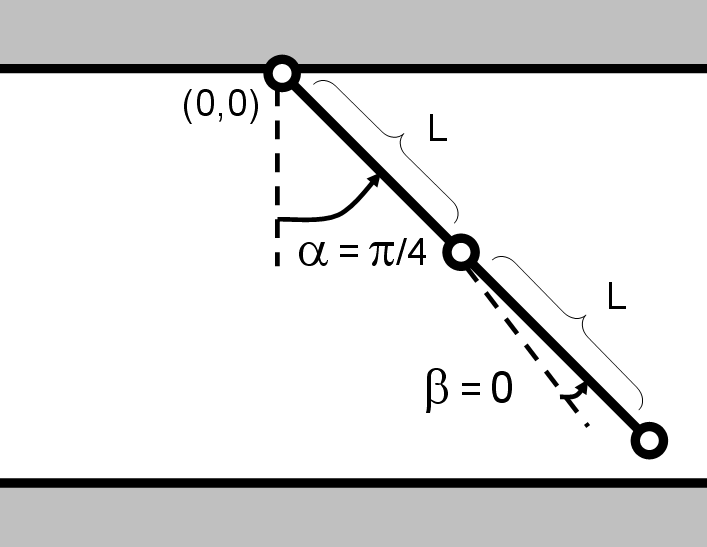
Question 5 (5 points). Consider the idealized ceiling-mounted robot shown below. It has two rotational joints, measured as shown, and for simplicity
you should ignore self-intersection issues (perhaps each arm segment has a slightly different z-coordinate). There is also a point articulator (perhaps a magnet or a very small claw) at the end of the
arm, which we will assume is always on (so it is not a degree of freedom). The task of the robot is to move from the start configuration: (α=-π/4, β=0) to
the goal configuration: (α=π/4, β=0), as shown below. Note that it cannot simply actuate α from -π/4 to π/4, since this will cause the actuator tip to collide with
the floor (you may assume the height of the ceiling is about 1.5L).
- How many degrees of freedom does the robot have? Draw the configuration space of the robot, marking the start (s) and goal (g) configurations. Label your axes clearly.
- Assuming the arm segments have length L and the ceiling mount is the origin, write out equations which give the mapping between configurations (α, β) and articulator positions (x,y).
- Is this mapping invertible? If yes, why? If no, give an example.
- Draw the free space by filling images of the floor and ceiling in configuration space (mark which regions are which).
- In your free space, there should be two kinds of reasonable paths from the start to the goal. Why? Sketch (in three or four frames) what physical motions correspond to these two kinds of paths.